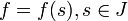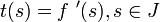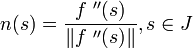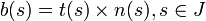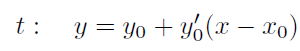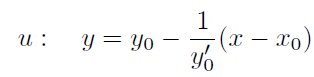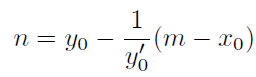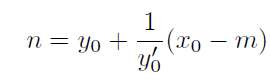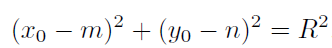Diferenciální geometrie křivek

Diferenciální geometrie je poměrně mladá oblast matematiky, bohatě rozvětvená, s vlastním aprátem, který přináší mnoho hlubokých výsledků. Ve svých počátcích, byla především disciplínou, v níž se geometrické problémy řešili pomocí výsledků matematické analýzy. Nejprve se studovaly vlastnosti křivek a ploch v euklidovském prostoru. Řada geometrických pojmů (např. tečna, objem, obsah) mohla být přesně definována teprve po zavedení pojmu derivace (Newton, Leibnitz) a intgrace. Vznik samostatné diferenciální geometrie je v 18. století spojován především se jmény L. Euler a G. Monge. K velkému rozvoji diferenciální geometrie došlo v 19. století a zasloužili se o něj především K. F. Gauss a B. Riemann. Od přelomu 19. a 20. století začala vývoj diferenciální geometrie značně ovlivňovat Einsteinova obecná teorie relativity.
Jedním z ústředních pojmů diferenciální geomterie je pojem křivky. Je rovněž součástí matematického aparátu užívaného v mechanice, nezbytný je i v matematické analýze (křivkový integrál). V zásadě je možný dvojí přístup, „kinematický“ a „statický“. V řadě konkrétních situací, křivku vytváříme pohybem s jedním stupněm volnosti (pohyb letadla na obloze, pohyb hrotu tužky po papíře), křivka poté vzniká jako trajektorie pohybu. Jindy zase můžeme křivku vnímat jako hotový celek, tedy jako jednorozměrný útvar (oblouk mostního pilíře, kolejová trať). Z mechaniky vzniká například představa o křivce jako o dráze pohybujícího se bodu, jehož souřadnice jsou
závislé na čase t.

Definice křivky

Křivka je v matematice geometrický jednorozměrný objekt, případně zobrazení úsečky do nějakého metrického prostoru.

Pokud bychom chtěli nějakou formálnější definici křivky, může znít takto:
Nechť M je nějaký matematický prostor a I interval reálných čísel, pak křivkou k rozumíme spojité zobrazení z I do M. Pokud má smysl hovořit o derivaci k říkáme, že křivka je hladká (nebo diferenciální). Hladká křivka je regulární, pokud se její derivace v žádném bodě nerovná nule. O uzavřené křivce pak můžeme hovořit, pokud je interval I uzavřený [a, b] a k(a) = k(b).

Rovinná křivka

Způsoby zadání rovinné křivky:

parametrické rovnice X(t) = [x(t), y(t)]
implicitní rovnice F (x, y) = 0
explicitní rovnice y = f(x)
kartézské souřadnice:

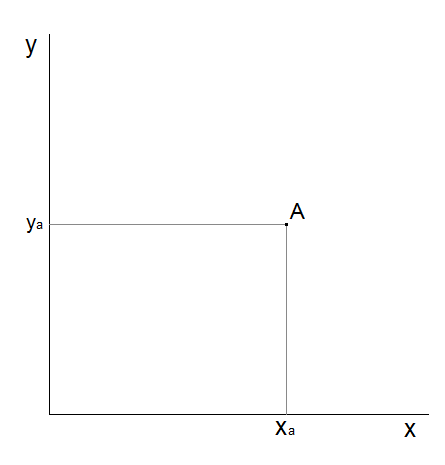
Obr. 1 - Kartézské souřadnice

polární souřadnice:

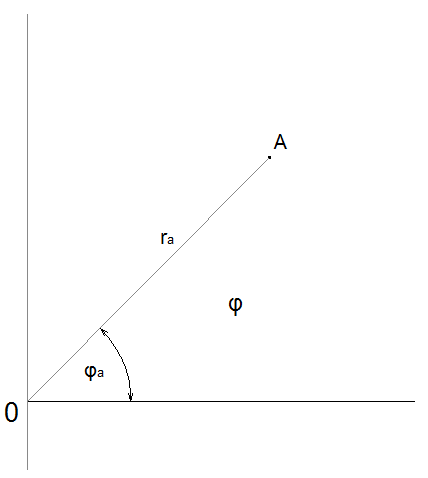
Obr. 2 - Polární souřadnice
x = r . cos φ
y = r . sin φ , φ ≥ 0

Jordanova definice křivky:

Rovinou křivku nazveme soubor bodů X = [x,y] v rovině, jejiž souřadnice jsou dány rovnicemi:

x = φ (t); y = ψ (t)

kde φ a ψ jsou spojité funkce proměné t ∈ (0;1)

Pokud bychom na proměnou t nahlíželi jako na čas, pak bod X = [x,y] pohybující se v čase t ∈ (0;1) v rovině, opíše křivku. Tato definice zahrnuje spirálu, kružnici, lomenou čáru i mnohé další objekty. Souřadnice bodu křivky jsou dány parametrickými rovnicemi, kde parametr nemusí být nutně čas, ale např. Úhel, délka oblouku, apod. Ze spojitosti funkcí φ a ψ plyne , že Jordanovy křivky jsou souvislé objekty, které nelze dělit na dvě disjunktní množiny (dvě množiny A a B jsou disjunktní právě tehdy, pokud je jejich průnikem prázdná množina). Pokud je objekt nesouvislá množina, pak musíme uvažovat jednotlivé souvislé komponenty. Z toho plyne, že například hyperbola, která má dvě větve, je Jordanovou křivkou.
Pokud existují pro funkce φ a ψ spojité derivace φ´ a ψ´, můžeme určit délku Jordanovy křivky:

Některé rovinné křivky

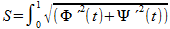
Jednou z nejjednodušších rovinných křivek je přímka. Jedná se o nekonečně tenkou, dvoustraně nekonečně dlouhou, dokonale rovnou křivku, tedy křivku s nekonečně dlouhým poloměrem zakřivení.

Kuželosečka je rovinná křivka, která vznikne jako průnik roviny s pláštěm rotačního kuželu, přičemž rovina neprochází jeho vrcholem.
Protínáme-li kužel rovinou kolmou na osu symetrie rotačního kuželu, výslednou kuželosečkou je kružnice.
Protínáme-li kužel rovinou rovnoběžnou právě s jednou z povrchových přímek pláště kuželu, výslednou kuželosečkou je parabola.
Protínáme-li kužel rovinou, která svírá s osou symetrie rotačního kuželu úhel menší než 90° a větší než polovina vrcholového úhlu kuželu, výslednou kuželosečkou je elipsa. Rovina přitom protíná všechny povrchové přímky pláště kužele a není tedy s žádnou z nich rovnoběžná.
Protínáme-li kužel rovinou, která svírá s osou symetrie rotačního kuželu úhel menší než polovina vrcholového úhlu kuželu, výslednou kuželosečkou je hyperbola; přitom rovina je rovnoběžná právě se dvěma povrchovými přímkami kuželu.

Obr. 3 - Kuželosečky

Spirála je rovinná křivka, která představuje trajektorii bodů pohybujících se po přímce podle daného pravidla, zatímco přímka se otáčí konstantní rychlostí kolem pevného bodu. Jedná se tedy o množiny bodů, jejichž vzdálenost ρ od pevného bodu O je funkcí velikosti úhlu α, který svírá rádiusvektor bodu spirály s pevně danou polopřímkou s počátkem v bodě O. K popisu spirál je tedy vhodné vyjádření v polárních souřadnicích ρ = f(α).
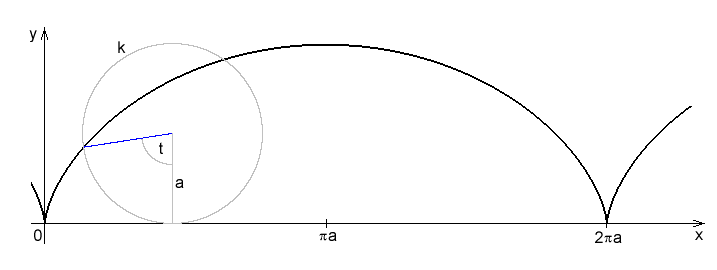
Se spirálami je možno se setkat prakticky všude. Jedním z prvních, kdo před 2300 lety popsal tuto křivku, byl Archimédes. Tzv. Archimédova spirála se vyskytuje např. jako trajektorie pohybu bodu, který se pohybuje po polopřímce od jejího počátečního bodu v pólu O konstantní rychlostí, zatímco polopřímka se sama otáčí kolem pólu při konstantní úhlové rychlosti . Archimédova spirála se také vyskytuje v různých mechanismech ve strojnictví jako tzv.Archimédův šroub (technicky se této křivce říká závitnice). Dále se můžem setkat například se spirálou Logaritmickou, Hyperbolickou, Fermatovou a Lituovou, Cornutovou,...

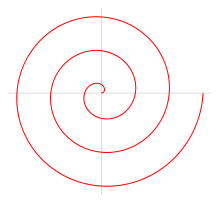
Obr. 4 - Archimedova spirála

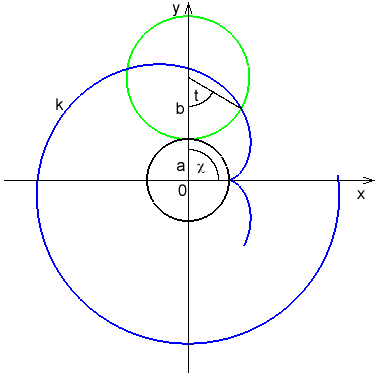
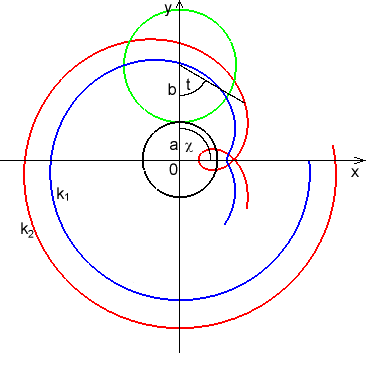
Klotoida je křivka, jejíž vlastnosti se užívají především v silničním stavitelství, kde se využívá jako přechodnice (při přechodu přímého úseku do úseku oblouku a naopak). Další název pro tuto křivku, se kterým se můžeme setkat např. při matematickém popisu difrakčních jevů, je tzv. Cornutova spirála.
Klotoida je tedy křivka, jejíž poloměr křivosti R v bodě M je nepřímo úměrný délce s oblouku mezi tímto bodem a pevně zvoleným bodem O tj.: R = a² / s, kde konstanta a je parametr, který určuje poměrnou velikost křivky.

Obr. 5 - Klotoida

Množina všech bodů roviny, které mají konstantní součin vzdáleností od dvou pevných bodů F₁,F₂ ,tzv. ohnisek, se nazývá Cassiniova křivka. Cassini se domníval, že po jedné z těchto křivek obíhá Země kolem Slunce. Křivka λ = a má své vlastní jméno - lemniskáta. Lemniskátu vykreslují křidélka letící mouchy, přibližně ji opisují meandrující řeky, oblouky lemniskáty najdeme rovněž u železničních přechodnic.

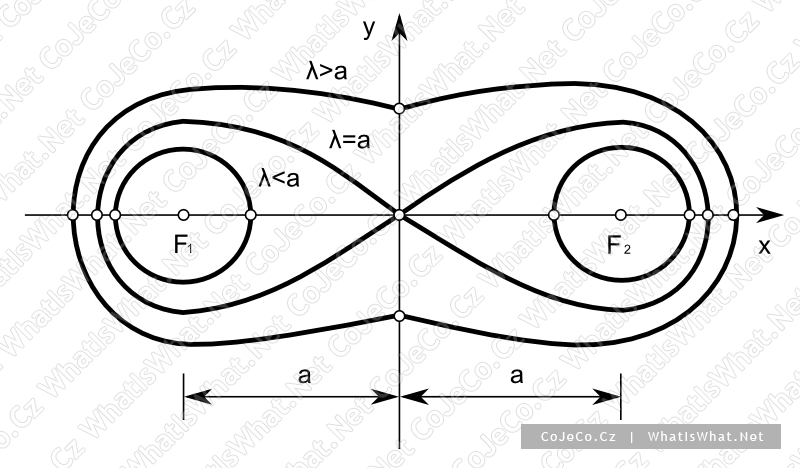
Obr. 6 - Cassiniho křivky

Cykloida je cyklická křivka, kterou vytvoří bod pevně spojený s kružnicí, která se valí (kutálí) po přímce. Cykloida má tvar donekonečna se opakujících oblouků.

Obr. 7 - Cykloida

Epicykloida vznikne jako dráha bodu pevně spojeného s kružnicí, která se odvaluje po vnější straně jiné, nehybné kružnice. Pokud bod leží na odvalující se kružnici, vzniká prostá Epicykloida. Pokud leží uvnitř, resp. vně odvalující se kružnice, vzniká zkrácená, resp. prodloužená Epicykloida.

Obr. 8 - Epicykloida

Hypotrochoida je křivka, kterou opisuje bod, spojený s kružnicí, odvalující se po vnitřku jiné, větší kružnice.

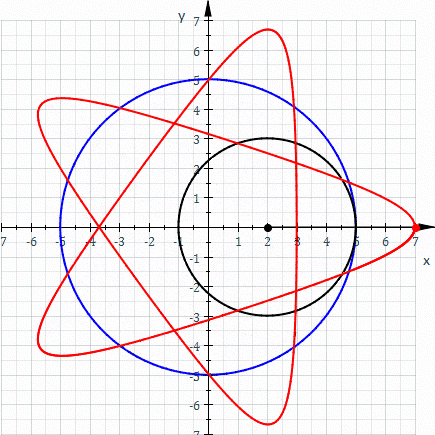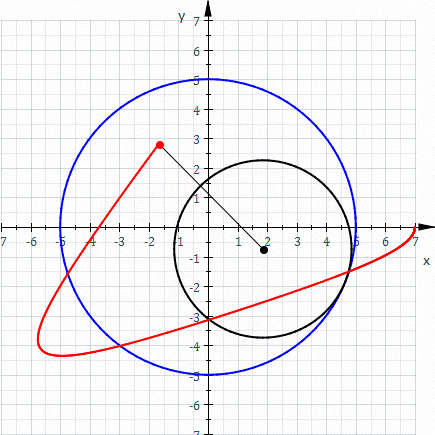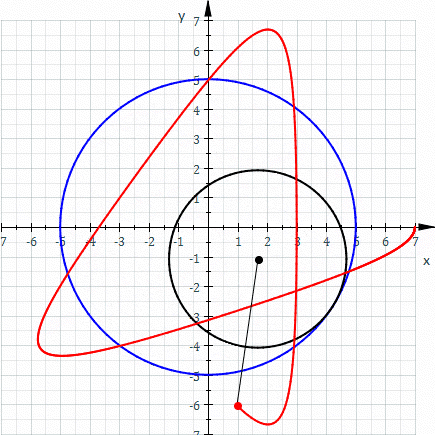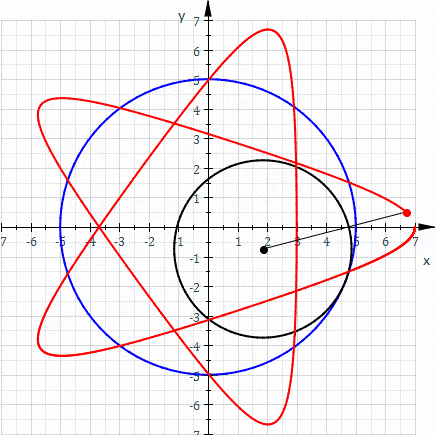
Obr. 9 - Hypotrochoida

Hypocykloida je cyklická křivka, kterou vytvoří bod pevně spojený s kružnicí, která se valí (kutálí) po vnitřní straně nehybné kružnice. Hypocykloida je speciálním případem hypotrochoidy.
Asteroida je rovinná křivka, kterou získáme jako speciální případ hypocykloidy.

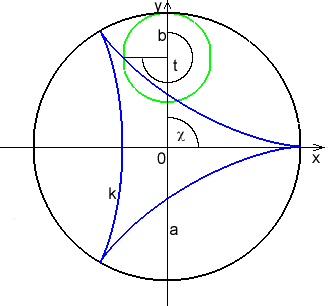
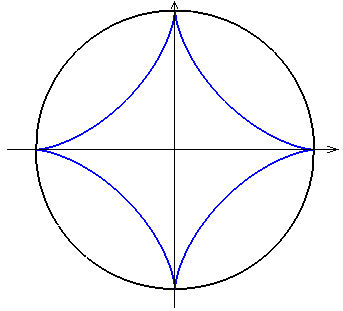
Obr. 10 - Hypocykloida a Asteroida

Prostorová křivka

Prostorovou křivkou rozumíme zobrazení: x = x(t) y = y(t) z = z(t) pro t = ( a, b), kde x, y a z jsou spojité funkce. Tyto uvedené rovnice křivky, bývají často zadávané ve vektorovém tvaru:
r = r(t) – kde r je polohový vektor (spojnice počátku souřadnic a hmotného bodu s orientací k hmontému bodu) Křivku v prostoru, lze vedle parametrického vyjádření zadat i jako průsečnici dvou ploch:

z = f (x, y)
z =g (x, y)
nebo:
G (x, y, z) = 0
H (x, y, z) = 0

Pokud jsou rovnice, které popisují křivku algebraické (rovnice je tvořena polynomem n tého stuně), pak hovoříme o polynomální křivce. Pokud algebraické nejsou, jedná se o křivku transcendentní.

Některé prostorové křivky:

Vivianiho křivka je průnikem sféry a rotační válcové plochy o polovičním poloměru , přičemž jedna z tvořících přímek válcové plochy prochází středem sféry.

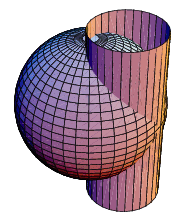
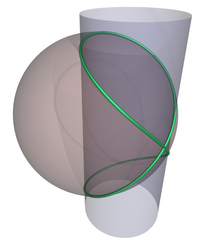
Obr. 11 - Vivianiho křivka

Šroubovice je jednou z nejdůležitějších křivek technické praxe. Definujeme ji jako dráhu bodu při šroubovém pohybu. Přitom šroubovým pohybem rozumíme pohyb složený z pohybu rovnoměrného otáčivého (rotačního) kolem přímky kolmé k rovině otáčení a rovnoměrného posuvného (translačního) ve směru této přímky (osy šroubového pohybu). Rovnoměrnost pohybu značí stálou velikost rychlosti, tj. velikost vektoru posunutí je přímo úměrná velikosti úhlu při pohybu otáčivém.

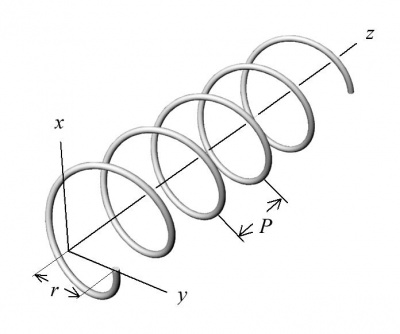
Obr. 12 - Šroubovice

Parametrizace křivky

Parametrizace (parametrické vyjádření nebo parametrické rovnice) křivek či ploch, určuje souřadnice bodů těchto geometrických útvarů jako funkce parametru. Jinými slovy, parametrické vyjádření určité křivky vytváří body této křivky. Parametrické vyjádření prostorové křivky vytváří průsečíky dvou ploch. Opakem parametrizace je implicitní vyjádření. To slouží k zjištění, zda určitý bod leží na dané křivce.

Příkladem může být parametrické a implicitní vyjádření jednotkové krůžnice:

Parametrické vyjádření: (cos a; sin a) - pro 0 ≤ a ≤ 2 π
Implicitní vyjádření: x² + y² = 1

Z parametrické rovnice rovnou získáme body na kružnici, např. pro a = 0,5 je to bod (cos 0,3; sin 0,3).
Z implicitního vyjádření lze určit, že např. bod (0,6; 0,8) leží na kružnici 0,6² + 0,8² = 1, naproti tomu např. bod (0,4; 0,9) na kružnici neleží, neboť 0,4² + 0,9² = 0,97 = 1.

Příklad 1.:
Křivka k je dána soustavou rovnic:

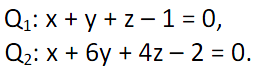
Napište parametrické rovnice křivky k.

Řešení: Každá z rovnic Qi je neparametrickou rovnicí roviny. Protože se jedná o různoběžné roviny, hledanou křivkou bude přímka. Zvolíme parametr např. x = t a dopočítáme y a z. Výsledkem je pak parametrické vyjádření přímky k:

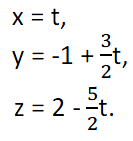
Příklad 2.:
Odvoďte parametrické rovnice prosté cykloidy

Řešení:Prostou cykloidou nazýváme křivku, která vznikne jako trajektorie bodu ležícího na obvodu kružnice, která se kutálí po přímce. Do kartézské soustavy souřadnic {O,x,y} umístíme kružnici se středem S =(0, r/2) a poloměrem r. Bod P je bodem ležícím na obvodu kružnice, jehož trajektorie popisuje vyšetřovanou křivku. Pravoúhlým průmětem bodu P do osy x, případně do osy y, je bod Q, případně R. Bod T je bodem dotyku kružnice a přímky. Parametr t určuje velikost úhlu TSP v obloukové míře při otáčení kružnice. Pro t=0 je P≡O≡T. Pro t>0 je délka oblouku TP rovna OT, proto OT = rt.

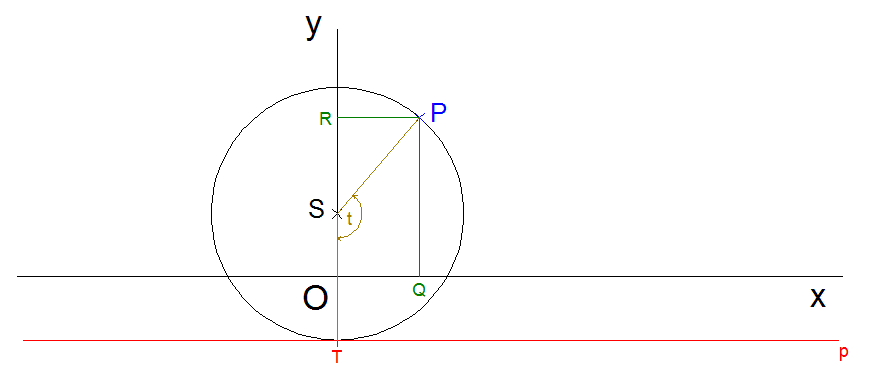
Obr. 13 - Kružnice opisující cykloidu

Pro x-ovou souřadnici bodu P platí:

x = OQ = OT – QT tj. x = rt – r sin t (protože QT = PR = r.sin t)

Pro y-ovou souřadnici bodu P platí:

x = QP = TS – RS tj. y = rt – r cos t (protože RS = r cos t)

Prostá cykloida je vyjádřena vektorovou funkcí: r(t) = (r (t-sin t), r (1-cos t)), pro t ∈ R

Parametrizace obloukem

Nechť P(t); t ∈ I = ( t_d; t_h ) je regulární křivka. Položme
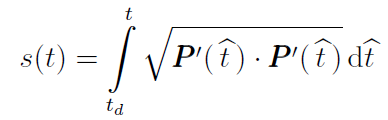
rovnice tečny

a inverzní funkci označme t(s). Pak nový parametr s nazýváme oblouk.

Definice vyplývá z faktu, že pro regulární křivku P(t); t ∈ I = ( t_d; t_h ) je délka křivky dána vztahem

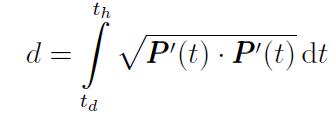
Příklad 3.:
Kružnici (0, r) parametrizujte obloukem.

Řešení Víme, že parametrické vyjádření kružnice je

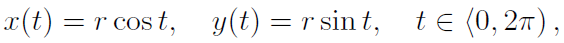
kde

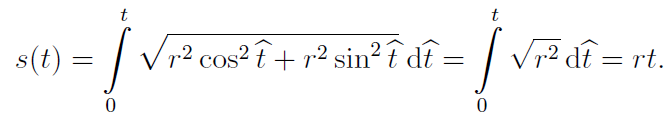
Pak dostáváme t = ( 1/r ) s a z toho plyne parametrizace obloukem ve tvaru

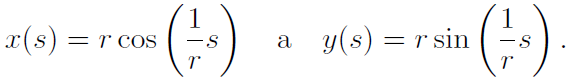
Tečna a normála

Tečna

Tečnu můžeme definovat jako přímku, která má s křivkou jeden společný bod dotyku. Na rozdíl od průsečíku, leží všechy okolní body křivky v polorovině, která je určena přímkou. Pokud je křivka grafem nějaké funkce, pak první derivace funkce je směrnice tečny.

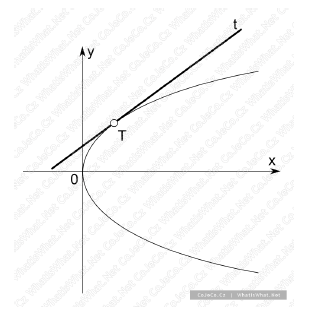
Obr. 14 - Tečna t ke křivce

Tečný vektor, je vektor tečny křivky, jejíž body jsou určeny polohovým vektorem r = r(t), která prochází bodem r₀= [x₀, y_0,z₀] dané křivky, tedy bodem, v němž má t = t₀ směr určený vektorem

Rovnici tečny ke křivce r = r(t) v bodě r₀ lze zapsat jako

nebo případně ve vektorovém tvaru jako

kde r₀= [x₀, y_0,z₀] je bod dotyku tečny R = [X, Y, Z], t je parametr křivky a u je parametr tečny.

Rovnici tečny ke grafu funkce můžeme zapsat takto: ( y - y_o ) = k . ( x - x_o )

Příklad 4.:

Napište obecnou rovnici tečny ke grafu funkce y = f(x) v bodě T.

Řešení: V bodě T známe souřadnici x_t = π / 2 a potřebujeme znát ještě souřadnici y_t.
Získáme ji dosazením x_t = π / 2 za x do vzorce funkce f(x)

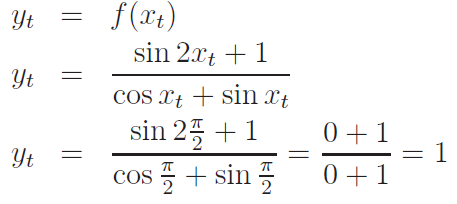
Teď už známe celý bod T = [ x_t, y_t ] = [ π/2, 1 ]. Víme, že tečna prochází bodem T. Dále v bodě T potřebujeme znát hodnotu derivace f´( x_t ). K tomu potřebujeme vypočítat derivaci f´(x) funkce f(x). Při výpočtu použijeme vzoreček pro derivaci podílu a vzoreček pro výpočet složené funkce.

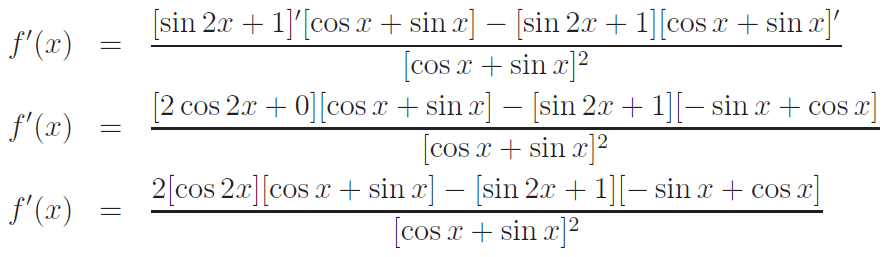
Derivaci by bylo možné dále upravovat, ale v tomto případě to není nutné. Stačí, když za x dosadíme hodnotu x_t = π / 2.

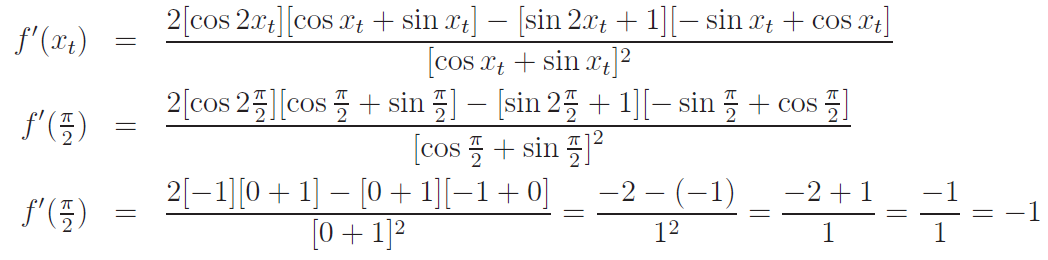
Teď už v bodě T známe hodnotu derivace f´( x_t ) = f´( π/2 ) = -1 . Víme o ní, že se rovná směrnici tečny v bodě T. Máme tedy všechny potřebné údaje o tečně, které můžeme dosadit do rovnice přímky ve vhodném směrnicovém tvaru.

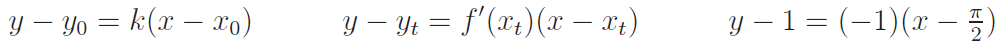
Směrnicový tvar rovnice upravíme na obecný tvar.

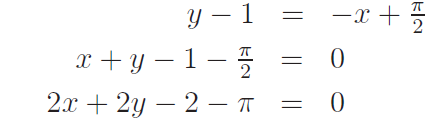
Normála

Všechny přímky, které prochází daným bodem křivky r = r(s),kde s je oblouk křivky, a jsou kolmé na tečný vektor t v tomto bodě, se označují jako normály křivky v daném bodě.

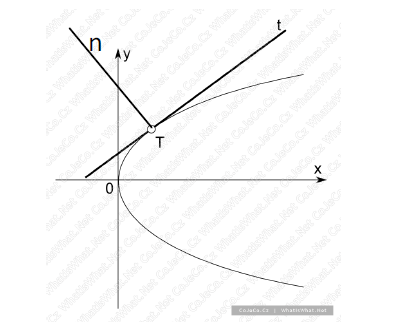
Obr. 15 - Normála ke křivce

Hlavní normálou křivky se nazývá přímka, která je její normálou v daném bodě a jejíž směr je určen vektorem dt / ds.

Jednotkový vektor n, který má stejný směr jako vektor dt / ds, se nazývá jednotkový vektor hlavní normály. Hlavní normála je definovaná pokud v hlavním bodě platí
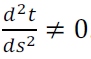hlnorm

.
vektor tečny a normálový vektor jsou vzájemě kolmé, tj. platí t . n = 0

Rovnice normály ke grafu funkce: ( y - y_o ) = - 1 / y_o ´ . ( x - x_o )

Frenetův doprovodný trojhran

Nazýván též Frenetův repér, je definován v každém regulárním neinflexním bodě křivky. Tvoří jej vektor tečny, hlavní normály a binormály křivky.

Nechť je křivka k třídy Cⁿ v prostoru E³ dána vektorovou rovnicí:

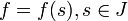
počáteční

jednotkový vektor

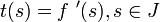
tečný vektor

nazýváme vektorem tečny křivky v bodě F (s). Tento vektor mění orientaci při přechodu k jinému oblouku, který mění orientaci křivky.
Rovina obsahující tečnu křivky se nazývá tečná rovina křivky.

jednotkový vektor

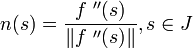
vektor normály

nazýváme vektorem hlavní normály v bodě F (s). Vektor hlavní normály je nezávislý na volbě oblouku.
Tečna a hlavní normála společně určují oskulační rovinu křivky.

jednotkový vektor

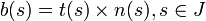
vektor binormály

nazýváme vektorem binormály křivky v bodě F (s). Binormála je tedy vektorový součin vektoru tečny a vektoru hlavní normály.Tento vektor je kolmý na vektor tečny a vektor hlavní normály.
Hlavní normála a binormála určují normálovou rovinu křivky. Tečna a binormála určují rektifikační rovinu křivky.

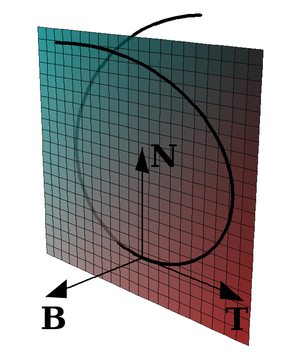
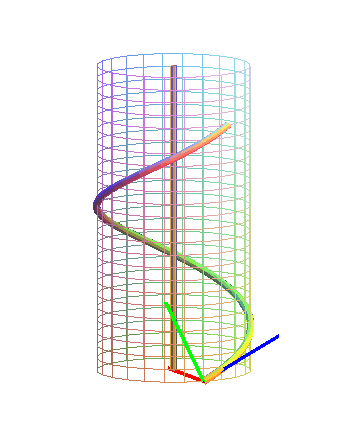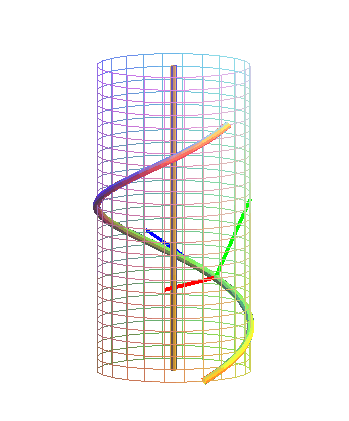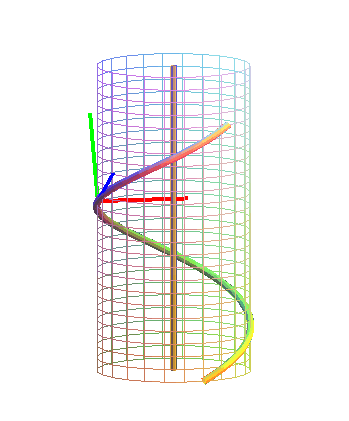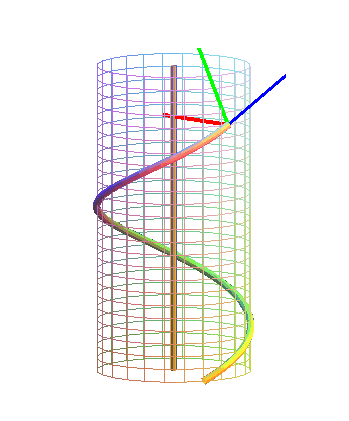
Obr. 16 - Frenetův repér

Oskulační kružnice, poloměr a střed křivosti

Mějme křivu AA´, která má v bodě M křivost rovnou K (viz. obr 12). Sestrojme tečnu a normálu křivky v bodě M. Postupně budeme bodem M prokládat kružnice, jejichž středy budou ležet na normále, ve směru, kterým je křivka vydutá. Všechny tyto body budou mít v bodě M společnou tečnu s křivkou AA´. Mezi těmito kružnicemi, existuje taková kružnice, která bude mít stejnou křivost K jako křivka v bodě M.
Ze vztahu mezi křivostí a poloměrem kružnice plyne, že poloměr zkoumané kružnice musí být roven absolutní hodnotě čísla 1 / k. Takto sestrojená kružnice se nazývá oskulační kružnice křivky v bodě M.

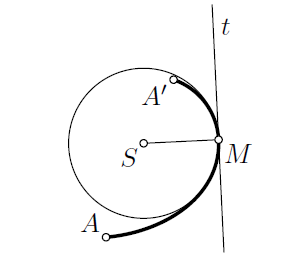
Obr. 17 - Oskulační kružnice

Převrácená hodnota křivosti v bodě M, tj R = 1 / K se nazývá poloměr křivosti a střed S oskulační kružnice se nazývá středem křivosti křivky v bodě M. Oskulační kružnice, tedy dává názornou představu o zakřivení křivky v daném bodě.

Výpočet středu křivosti.

Vycházíme z poznatku, že střed křivosti S leží na normále, která prochází bodem M = [ x₀ ; y₀ ] kolmo k tečně. Pro vzdálenost | SM | platí, že | SM | = R.

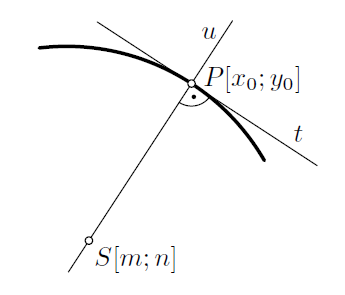
Obr. 18 - Střed křivosti

Rovnice tečny t je dána vztahem

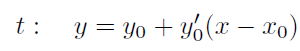
Rovnice normály u je pak dána vztahem

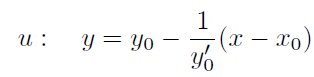
Protože bod S leží na normále u můžeme psát
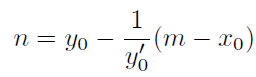
rovnice normály

po úpravě

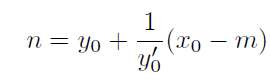
Protože bod M = [ x₀ ; y₀ ] leží na oskulační kružnici se středem S můžeme psát
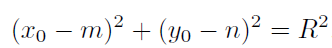
rovnice normály

Předchozí dva vztahy předtsavují soustavu dvou rovnic o dvou neznámých. Řešením této soustavy dostáváme
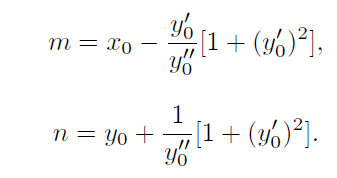
rovnice normály

Literatura

A. Vanžurová: Diferenciální geometrie křivek a ploch, Univerzita Palackého, 1996
L. Lomtatidze: Historický vývoj pojmu křivka, Česká matematická společnost, 2007
J. Pradlová: Diferenciální geometrie: sbírka řešených příkladů, Západočeská univerzita v Plzni, 2001
J. Bureš, K. Hrubčík: Diferenciální geometrie křivek a ploch, Nakladatelství univerzity karlovy 1998
L. Boček, V. Kubát: Diferenciální geometrie křivek a ploch, Státní pedagogické nakladatelství Praha 1983

Odkazy

I. Kolář, L. Pospíšilová: Diferenciální geometrie křivek a ploch, elektronická skripta - odkaz
http://www.fd.cvut.cz/department/k611/PEDAGOG/K611GM.htm
cs.wikipedia.org/wiki/
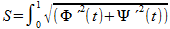
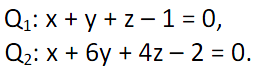
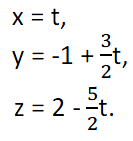
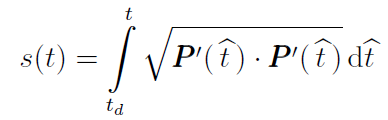
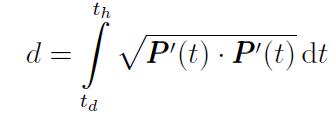
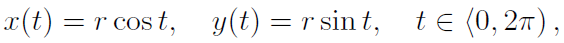
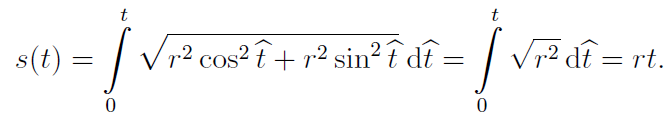
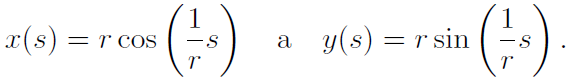
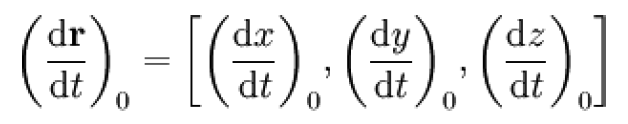
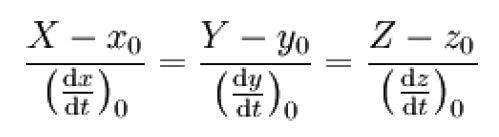
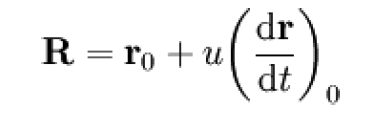
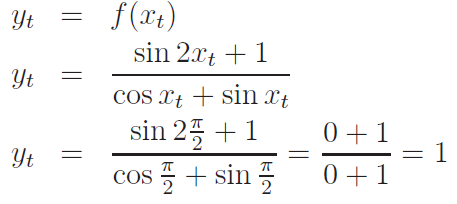
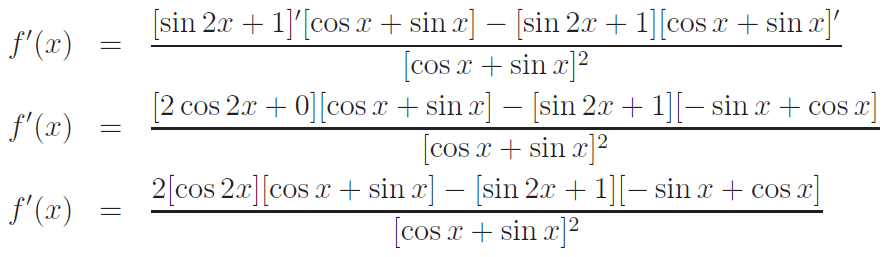
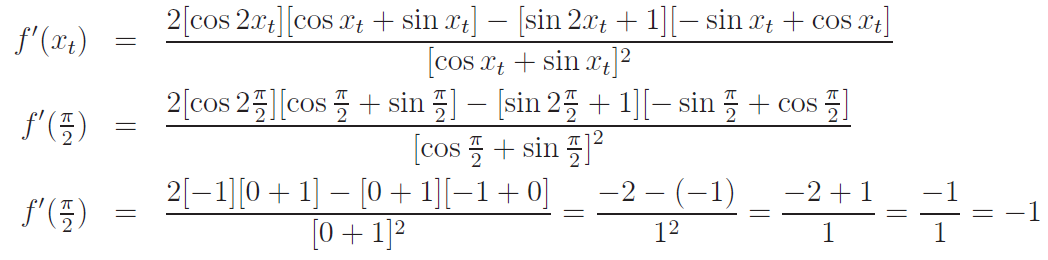
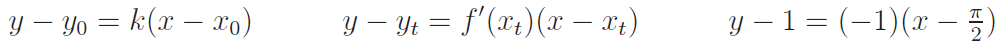
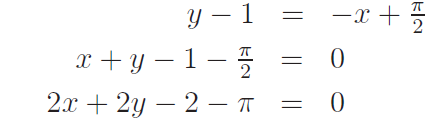