MONGEOVO PROMÍTÁNÍ
- podle Gaspard Monge 1746-1818
- nejběžnější zobrazení v deskriptivní geometrii
- pravoúhlé promítání na dvě k sobě kolmé průmětny
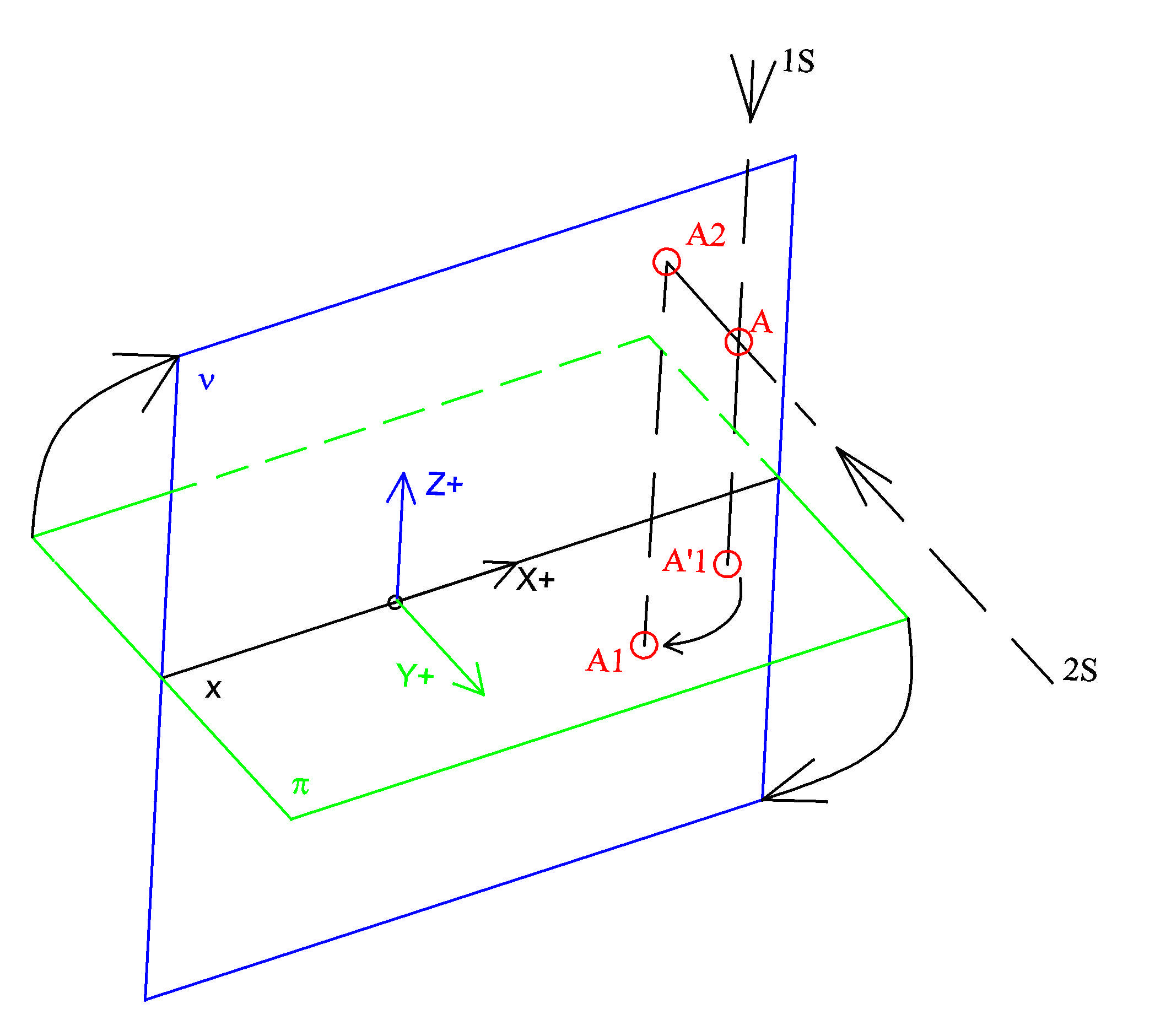
Zobrazení bodu
- zvolíme dvě k sobě kolmé průmětny =>půdorysnu π (vodorovná průmětna) a nárysnu ν (svislá průmětna)
- jejich stýkající se hranu (průsečnice) označme x a nazveme ji základnice
- kartézský souřadnicový systém umístíme tak, aby osa x splývala se základnicí x, osa y leží v půdorysně
a osa z v nárysně
- bod A v prostoru zobrazíme tak, že nejprve pravoúhle promítneme na nárysnu, nárysně promítacím paprskem 2S,
získáme nárys bodu A, který označíme A2
- pak bod A pravoúhle promítneme na půdorysnu, půdorysně promítacím paprskem 1S, tímto dostaneme první průmět
bodu A, označíme jej A´1
- abychom mohli tuto prostorovou situaci zobrazit v rovině, sdružíme průmětny tak, že otáčíme půdorysnu π,
aby záporná polorovina se přetočila na kladnou polorovinu nárysny
ν ,
(bod A´1se otočí do polohy A1) bod A1 nazveme půdorys bodu A, bod A jsme tak
zobrazili do dvojice sdružených průmětů A1 a A2
- tahle prostorová situaci se také jinak nazývá levotočivý souřadnicový systém, půdorysna π je otáčena po směru hodinových ručiček, tak jak je vysvětleno v předchozím odstavci
- promítací paprsky 1S a 2S bodu A navzájem vytvářejí rovinu kolmou k π, k ν a k x,
rovina je taktéž rovinou otáčení bodu A´1 do bodu A1, tedy spojnice A1, A2 je kolmá k základnici x
této spojnici půdorysu a nárysu (mezi body A1, A2) nazýváme ji ordinála
- protože se při otáčení | π | , kolem základnice x do ν | vzdálenosti průmětů bodů
od základnice zachovávají, můžeme říct, že orientovaná vzdálenost půdorysu bodu od základnice se rovná orientované vzdálenosti
bodu od nárysny a orientovaná vzdálenost nárysu bodu od základnice se rovná orientované vzdálenosti bodu od půdorysny
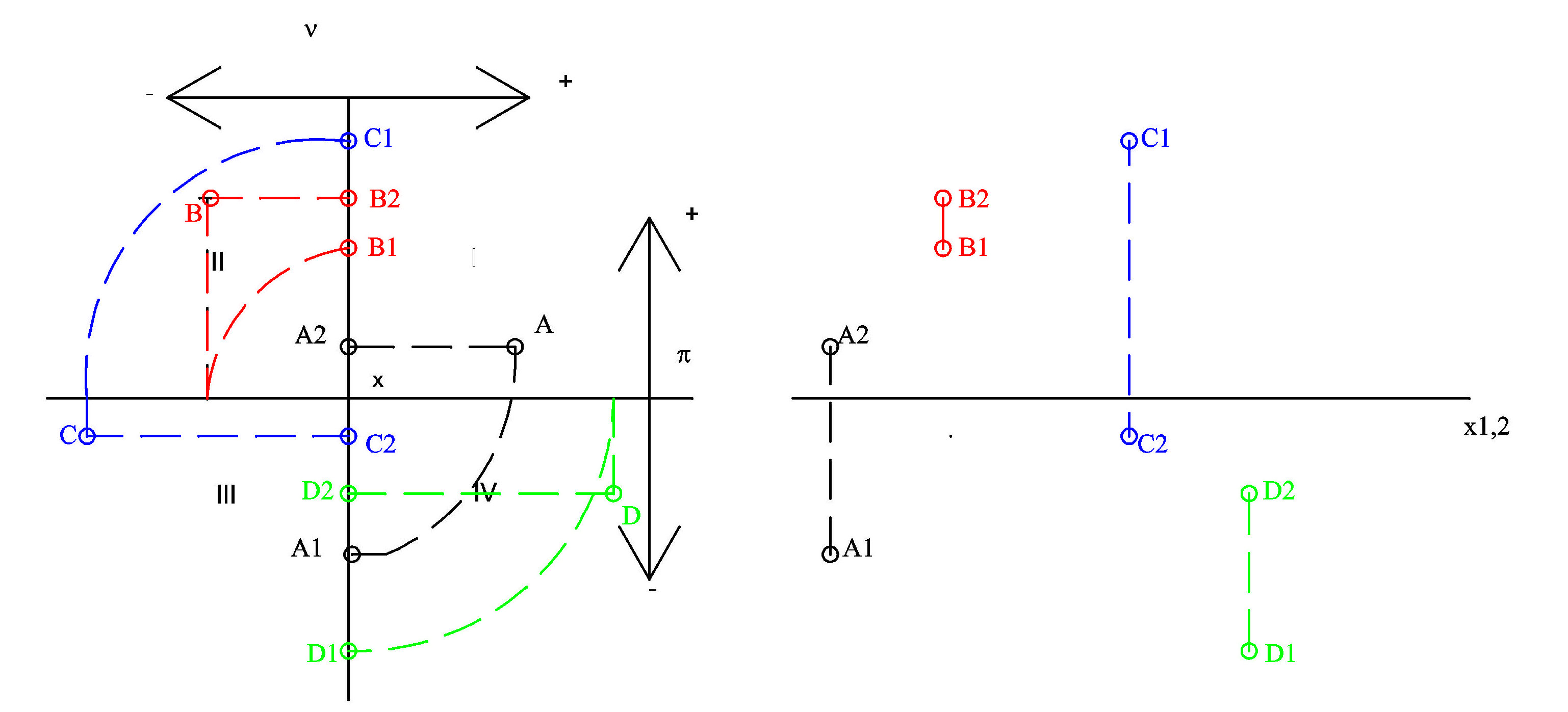
- obě k sobě kolmé průmětny rozděluje prostor na 4 kvadranty,podle znamének souřadnic bodů můžeme hned zjistit ve kterém
kvadrantu se bod nachází, pro znázornění si ukážeme body A,B,C,D ve všech čtyřech kvadrantech
<
Zobrazení přímky
- zobrazení přímky provedeme tak, že do průměten pravoúhle promítneme každý její bod, jestliže přímka:
a) je kolmá k průmětně, je jejím průmětem bod
b) není-li kolmá k průmětně, pak přímkou proložíme rovinu kolmou k průmětně (tzv. promítací rovinu přímky),
průmětem přímky je průsečnice průmětny a promítací roviny
- přímka je určena dvěmi ruznými body, sdružené průměty můžeme tedy určit pomocí sdružených průmětů těchto bodů
- průsečík přímky s průmětnou se nazývá stopník přímky
- přímka která není rovnoběžná s žádnou průmětnou ( π , ν , ω )se nazývá obecná přímka
- přímka rovnoběžná s průmětnou se nazývá hlavní přímka
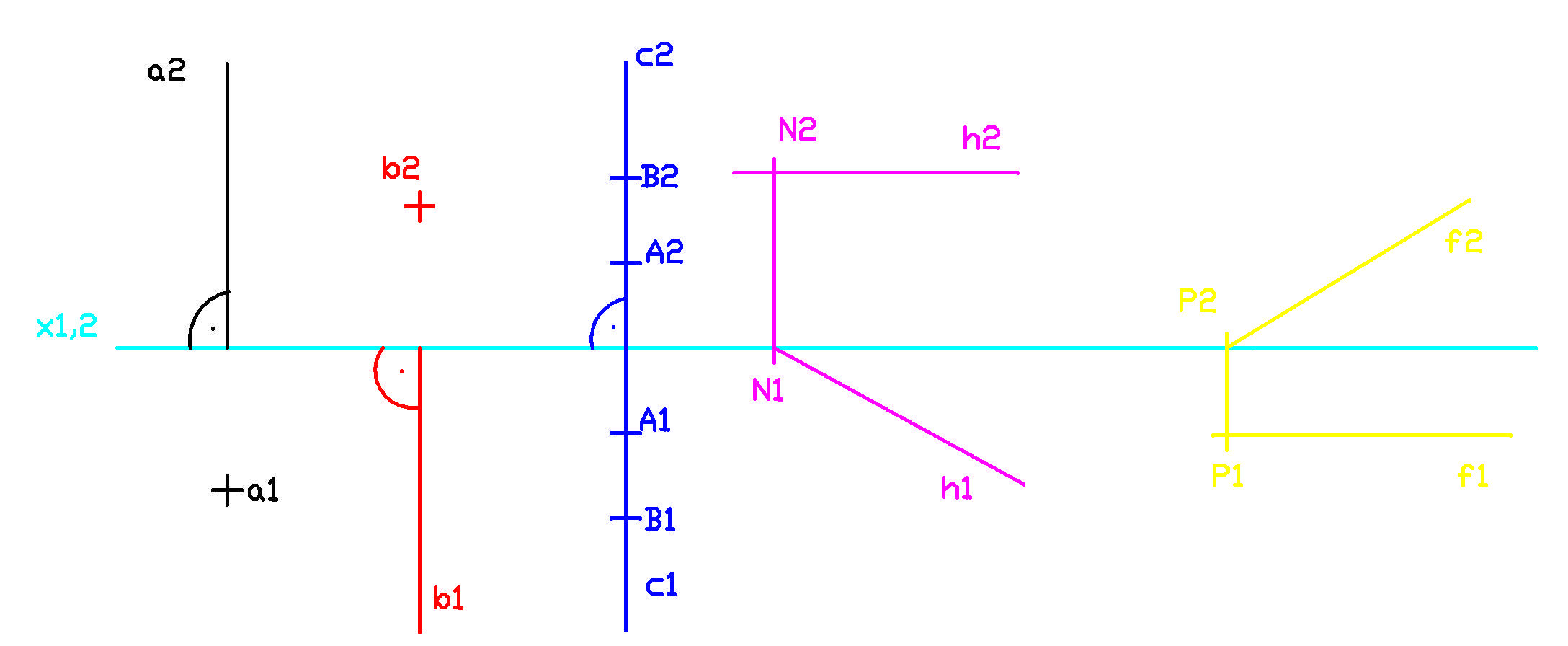
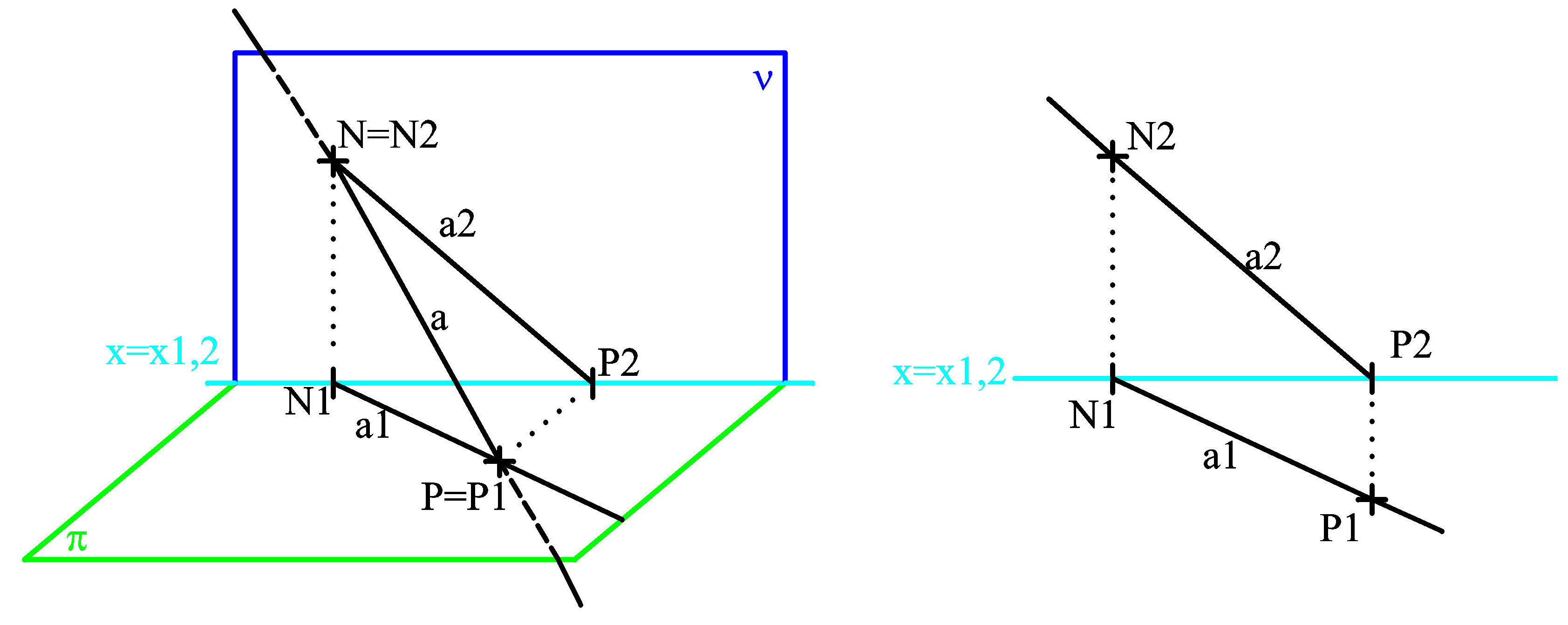
Základní pojmy:
- půdorys (první průmět) přímky a....a1
- nárys (druhý průmět) přímky a.....a2
- bokorys (třetí průmět) přímky a.....a3
- sdružené průměty přímky a.....a1,a2
- půdorysný stopník přímky a......P = a ∩
π |
- nárysný stopník přímky a......N = a ∩
ν |
- bokorysný stopník přímky a......M = a ∩
ω |
Polohy přímky
- sdružené průměty přímky, které nejsou kolmé k ose x, jsou přímky (různé nebo splývající),z nichž žádná není kolmá k základnici
- sdružené průměty přímky kolmé k průmětně jsou bod a přímka kolmá k základnici
- přímka kolmá k základnici, která není kolmá k žádné z průměten, není určena svými sdruženými průměty např:
průměty jejich dvou různých bodů
- nárysem přímky rovnoběžné s půdorysnou je buď přímka rovnoběžná se základnicí nebo bod
- půdorysem přímky rovnoběžná s nárysnou je buď přímka rovnoběžná se základnicí nebo bod
Speciální polohy přímky
Obr. Speciální (zvláštní) polohy přímky
- zapotřebí je také vědět, jak se zobrazují dvojice přímek ; máme tři druhy:
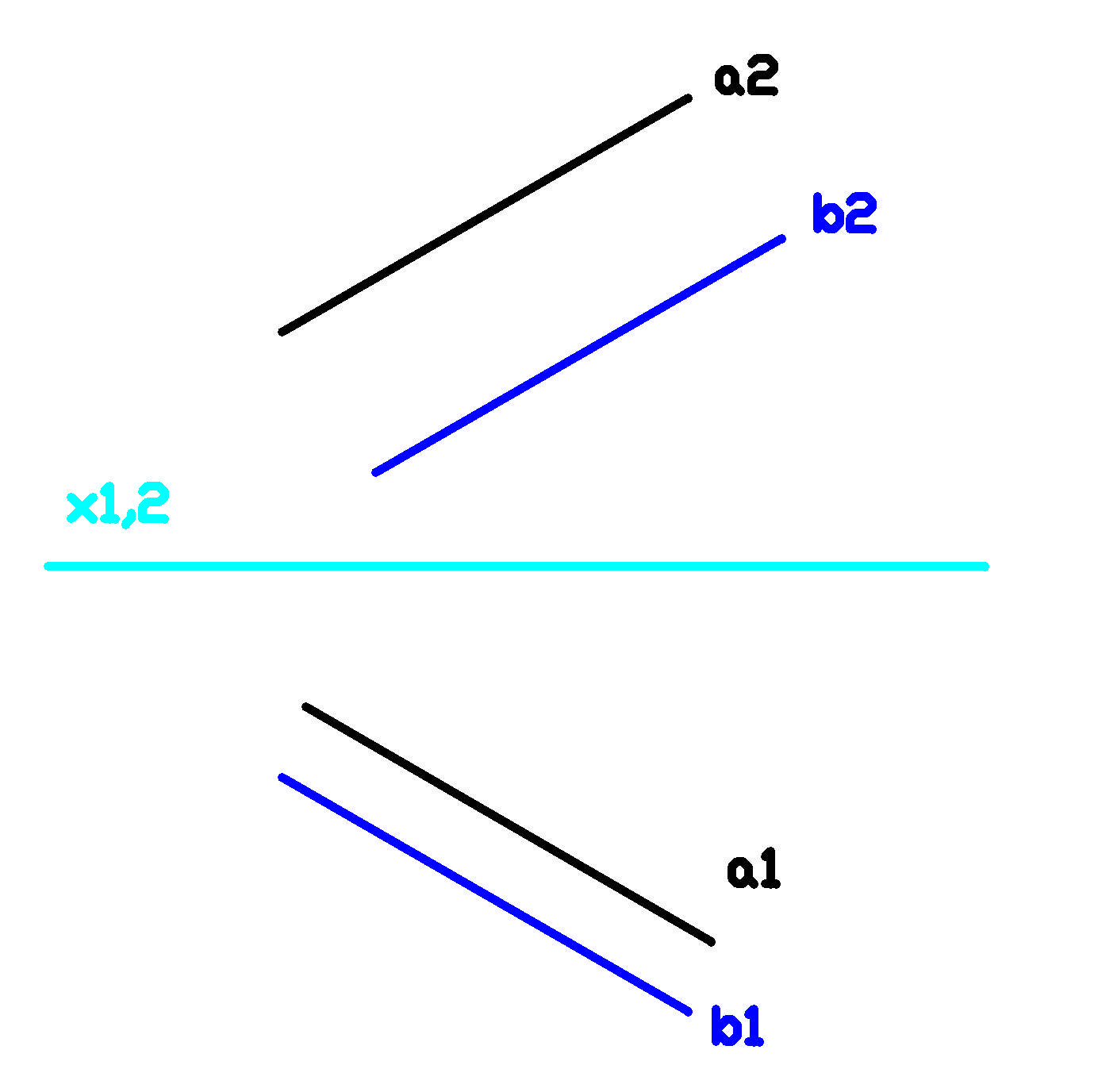
Obr. a) rovnoběžky; neleží-li v jedné promítací rovině, do
půdorysu i nárysu se zobrazí jako rovnoběžky (mají společný nevlastní bod)
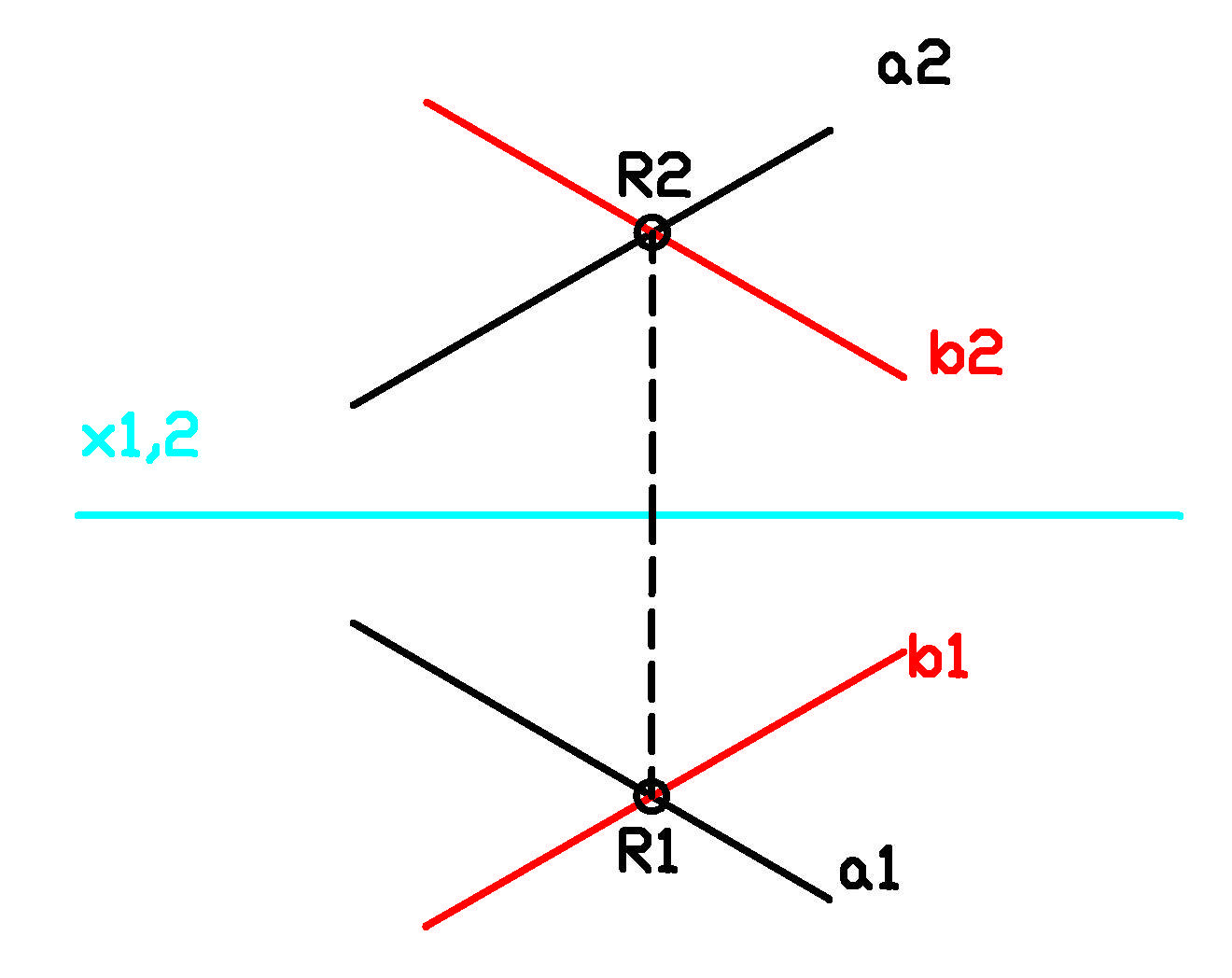
Obr. b) různoběžky, neleží v jedné promítací rovině, do
půdorysu i nárysu, se zobrazí jako různoběžky (mají společný vlastní bod)
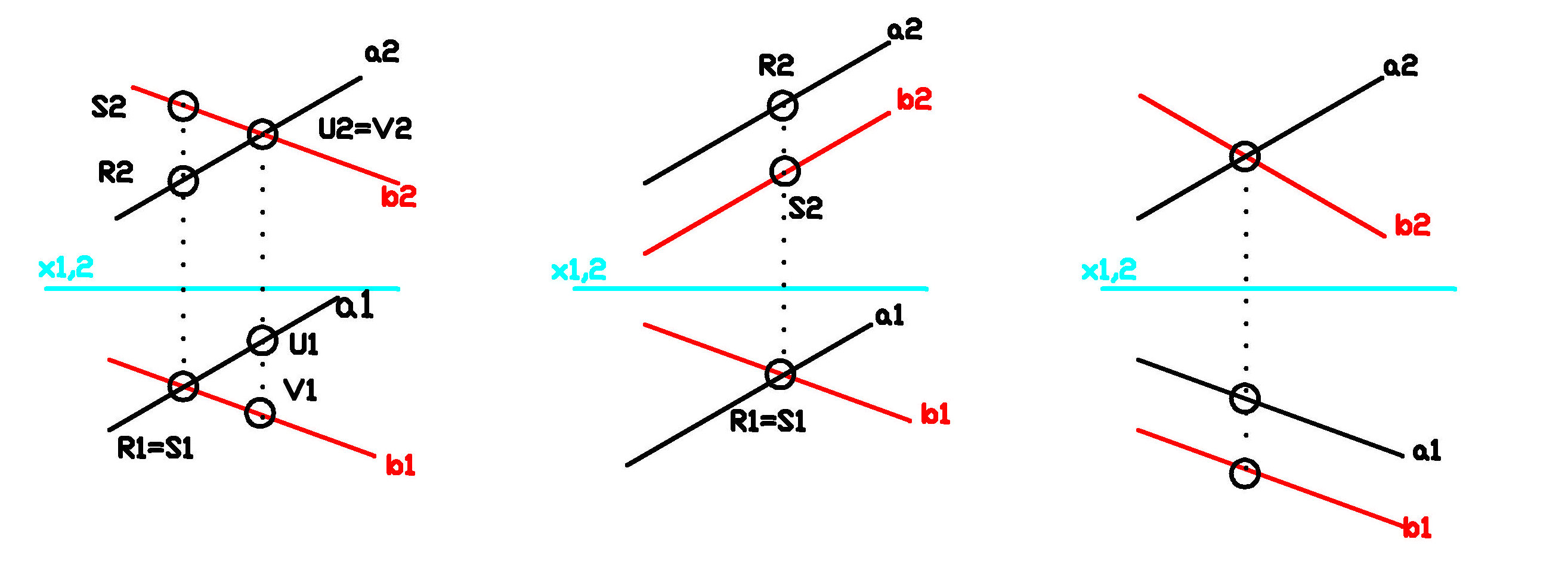
Obr. c) mimoběžky, se zobrazí buď jako v obou průmětech jako různoběžky,
nebo v jednom průmětu jako různoběžky a v druhém jako rovnoběžky (nemají společný bod)
Zobrazení roviny
- průmětem roviny, která není kolmá k průmětně, je celá průmětna (půdorysna, nárysna, bokorysna)
- průmětem roviny kolmé k průmětně je přímka
- rovina
α | kolmá k půdorysně (respektive k nárysně ) má svůj půdorys označen
α1 | (respektive α2 | )
-rovina není přímo určena svými průměty, proto pro zobrazování roviny používáme sdružené průměty jejich určujících prvků:
a) tří bodů které neleží na jedné přímce
b) přímky a bodu které na ní neleží
c) dvou různých rovnoběžných přímek
d) dvou různoběžných přímek
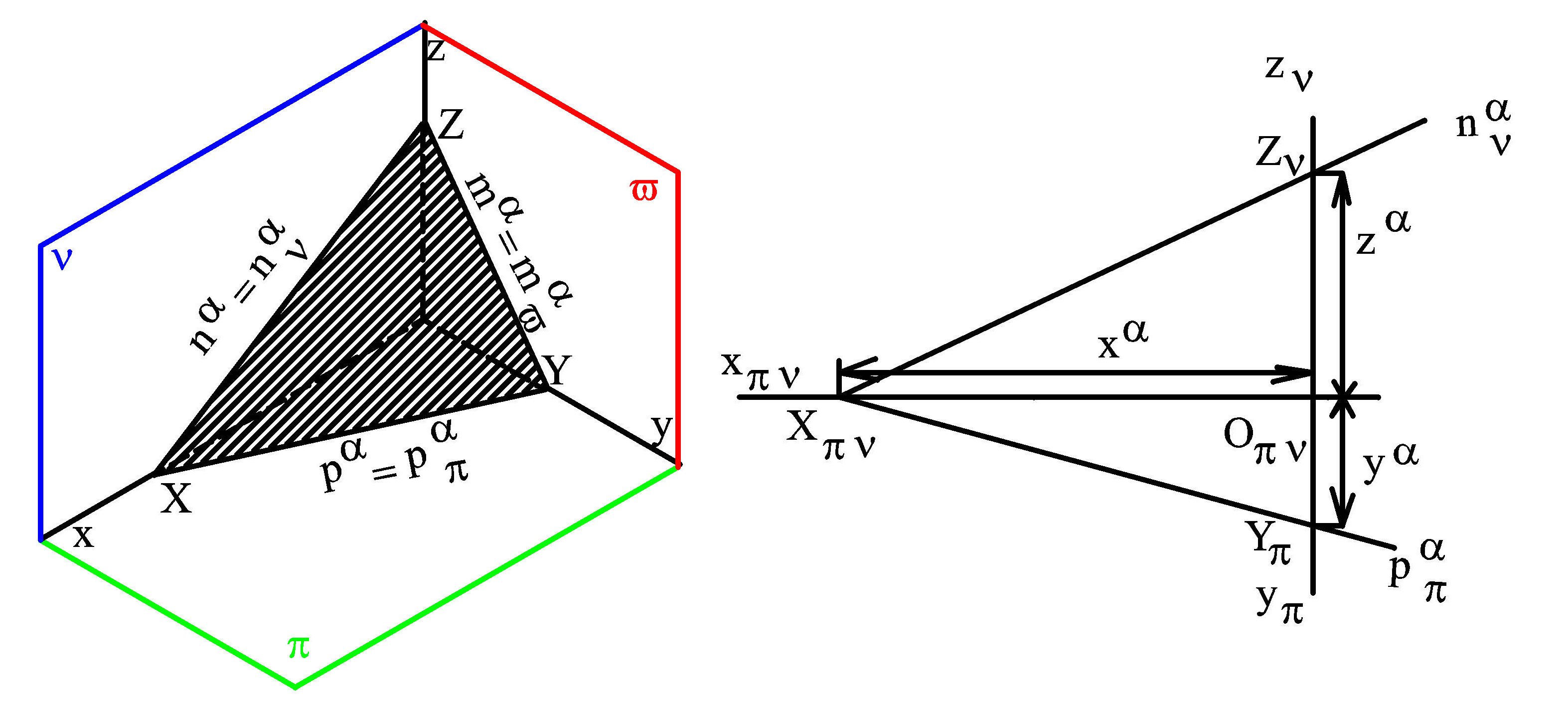
- obvyklým případem dvou určujících přímek jsou průsečnice roviny s dvěma průmětnami, tyto průsečnice se nazývají stopy roviny
- rovina, která není kolmá k žádné průmětně, se nazývá obecná rovina
Pojmy:
- půdorysná stopa roviny
α | .....p α | = α | ∩ π |
- nárysná stopa roviny
α | ...n α | = α | ∩ ν |
- bokorysná stopa roviny
α | .... m α | = α | ∩ ω |
- rovina rovnoběžná s průmětnou se nazývá hlavní rovina
- hlavní rovina rovnoběžná s půdorysnou je zřejmě kolmá k nárysně, můžeme ji tedy vzhledem nárysně promítnout a jejím
nárysem je přímka, protože je rovnoběžná s půdorysnou, je nárysem přímka rovnoběžná se základnicí
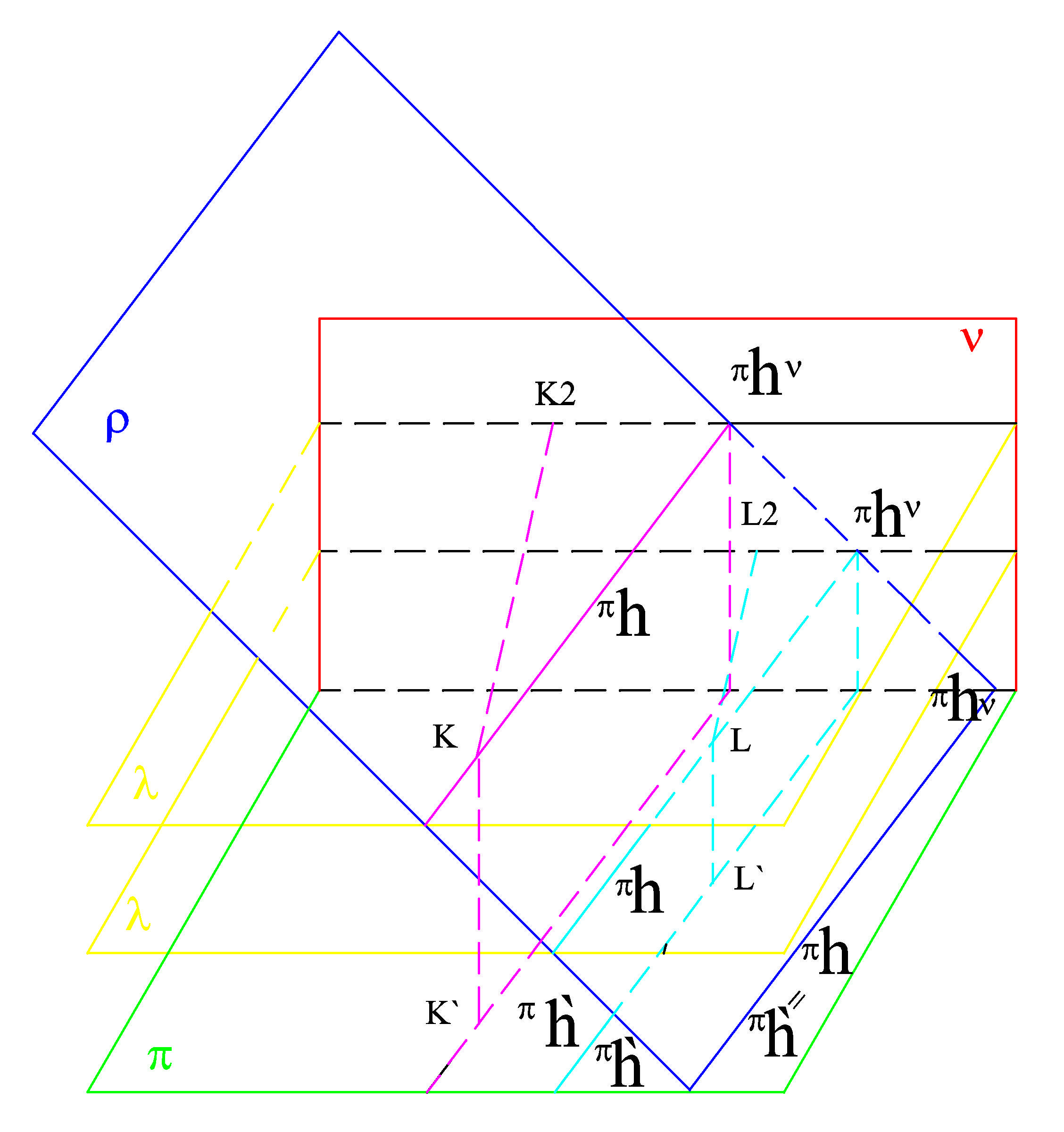
- rovina, která není hlavní, je hlavními rovinami křížena v hlavních přímkách, tyto hlavní přímky jsou vzájemě rovnoběžné
- hlavní přímky roviny jsou vzájemě rovnoběžné
- hlavní přímky roviny
ρ | , které jsou rovnoběžné s půdorysnou nazýváme hlavní přímky první osnovy
a značíme je π | h ρ | , hlavní přímky rovnoběžné s nárysnou nazýváme
hlavní přímky druhé osnovy a značíme je ν | h ρ |
- všechny přímky roviny, které jsou kolmé k jejím hlavním přímkám, se nazývají spádové přímky
- spádové přímky roviny
ρ | , které jsou kolmé k hlavním přímkám první osnovy, nazveme
- spádové přímky první osnovy a označíme je π | s ρ |
- spádové přímky roviny
ρ | , které jsou kolmé k hlavním přímkám druhé osnovy, nazveme
- spádové přímky druhé osnovy a označíme je π | s ρ |
- protože spádové přímky téže osnovy jsou vzájemně rovnoběžné, jsou i jejich průměty vzájemně rovnoběžné
Roviny ve speciální poloze vzhledem k průmětnám:
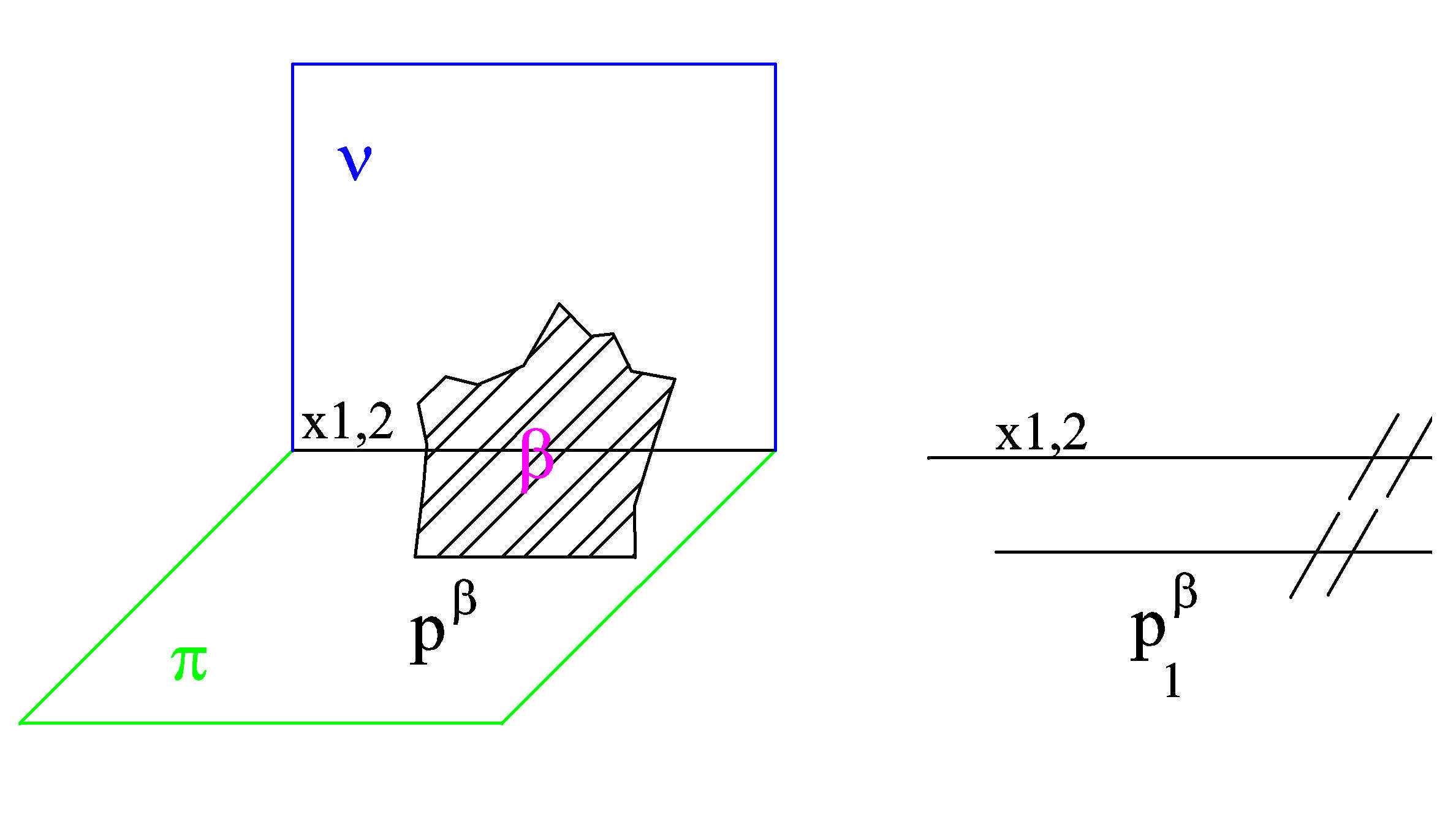
Obr. 1) rovina je kolmá k půdorysně a rovnoběžná s nárysnou - promítací rovina
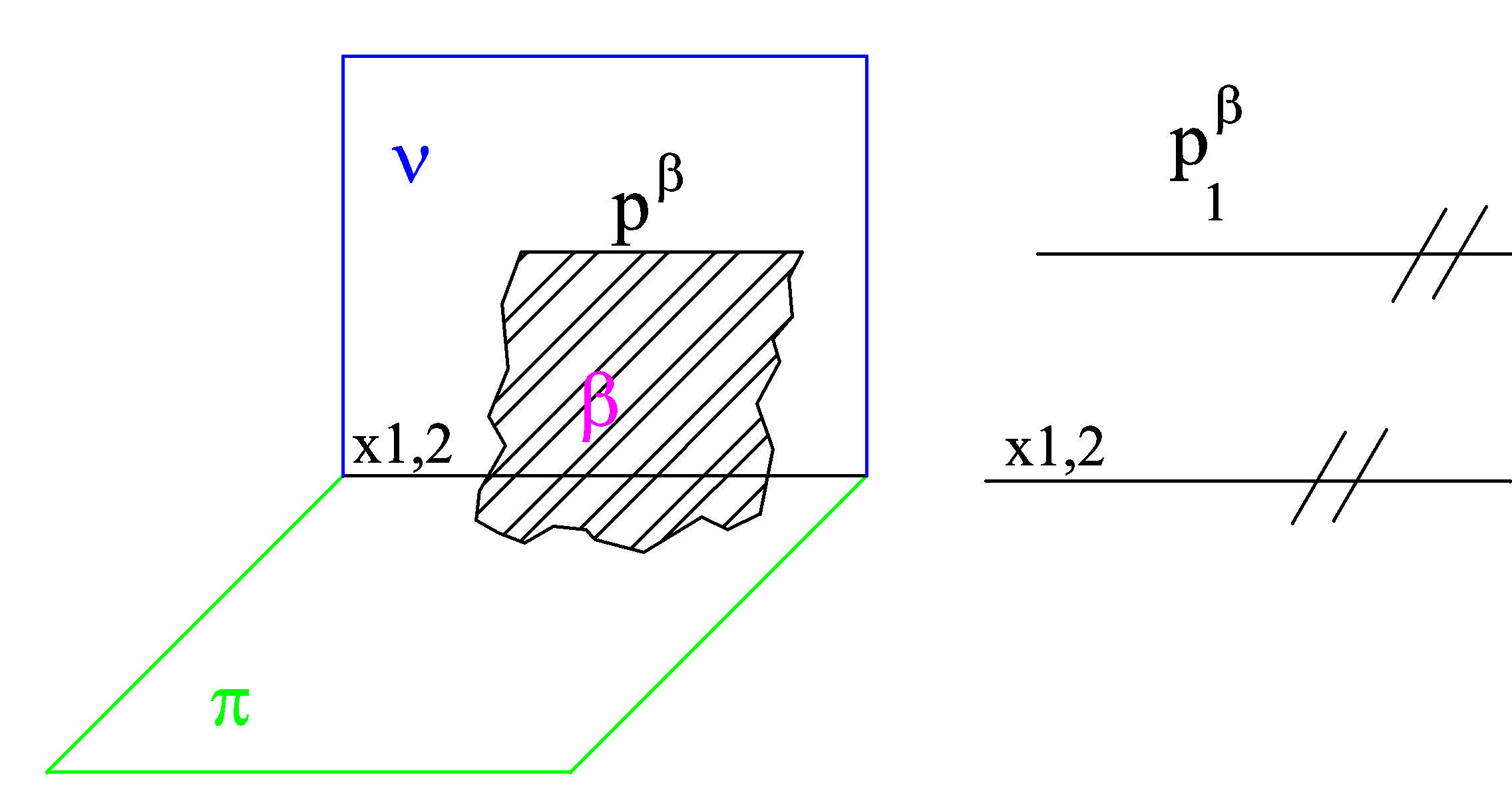
Obr. 2) rovina je kolmá k nárysně a rovnoběžná s půdorysnou - promítací rovin
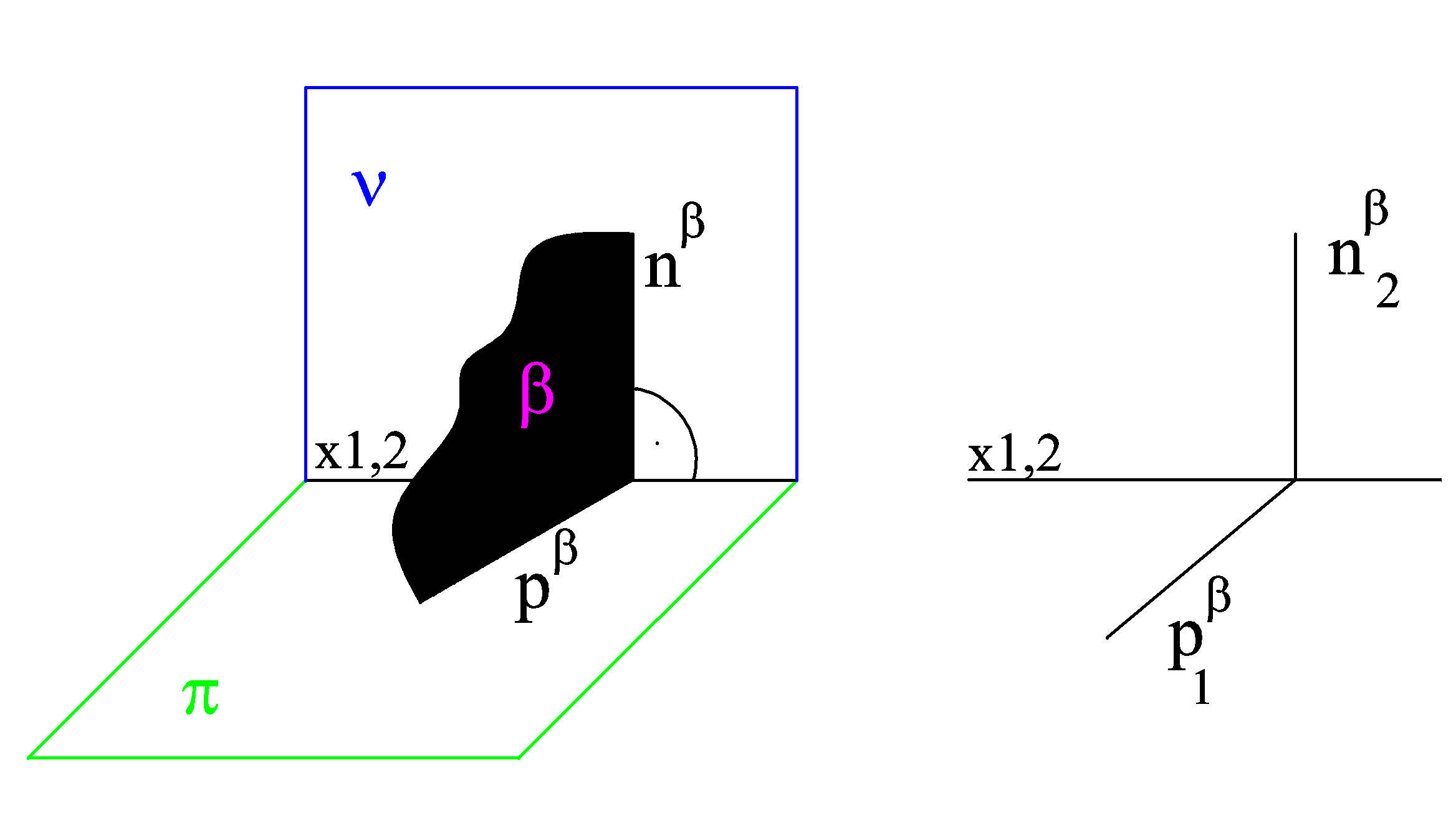
Obr. 3) rovina je kolmá k půdorysně a různoběžná s nárysnou - promítací rovina
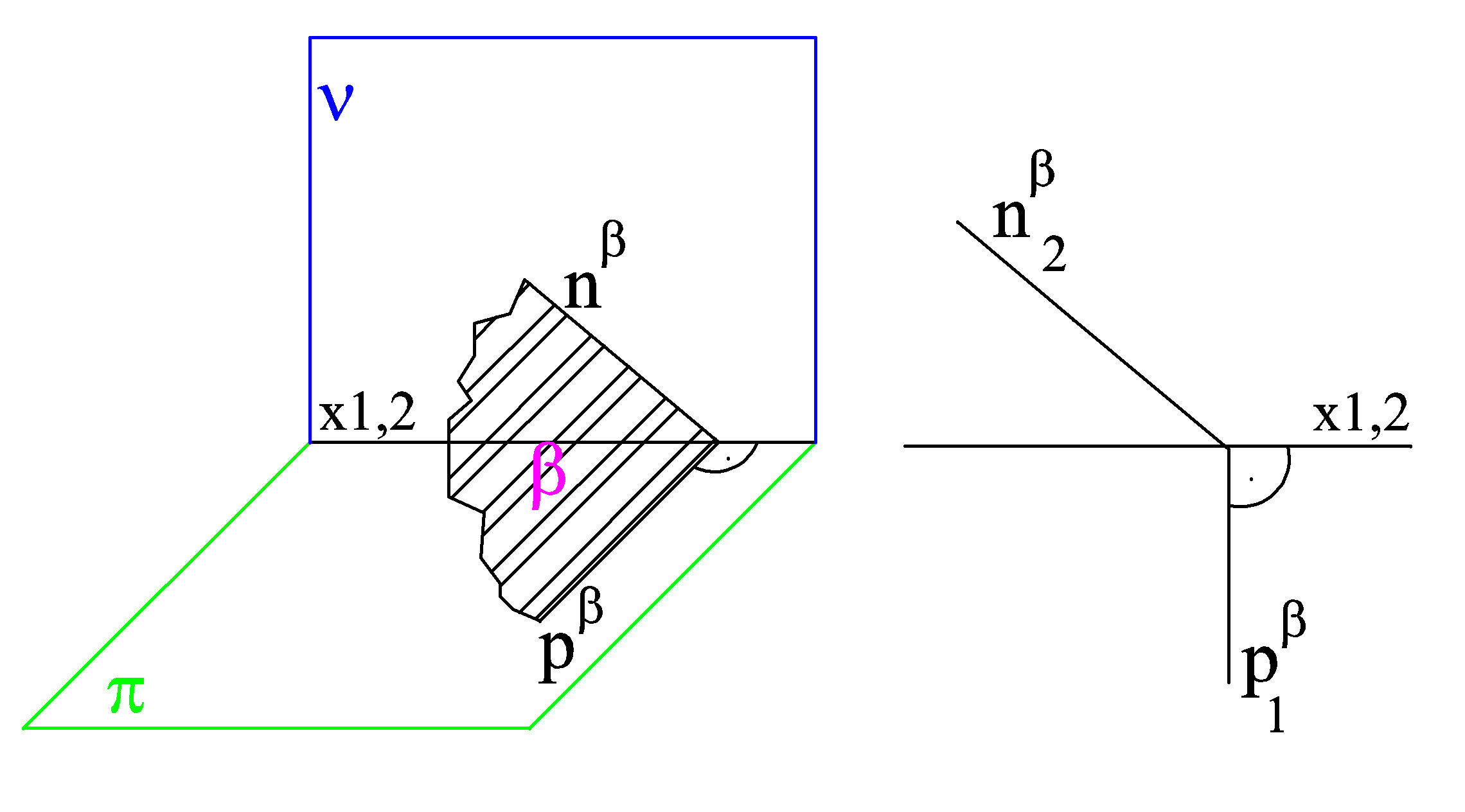
Obr. 4) rovina je kolmá k nárysně a různoběžná s půdorysnou - promítací rovina
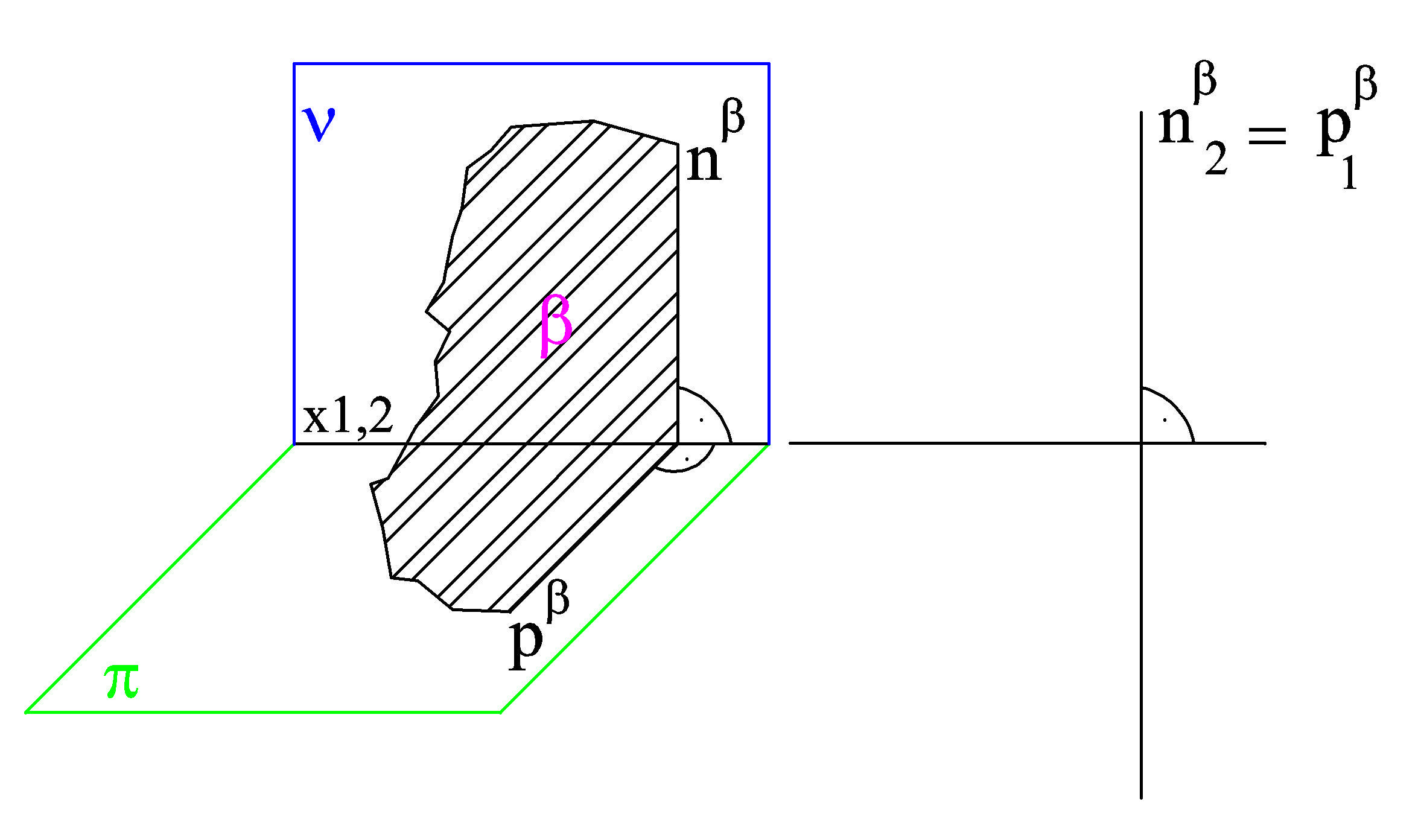
Obr. 5) rovina je kolmá k oběma průmětnám - promítací rovina
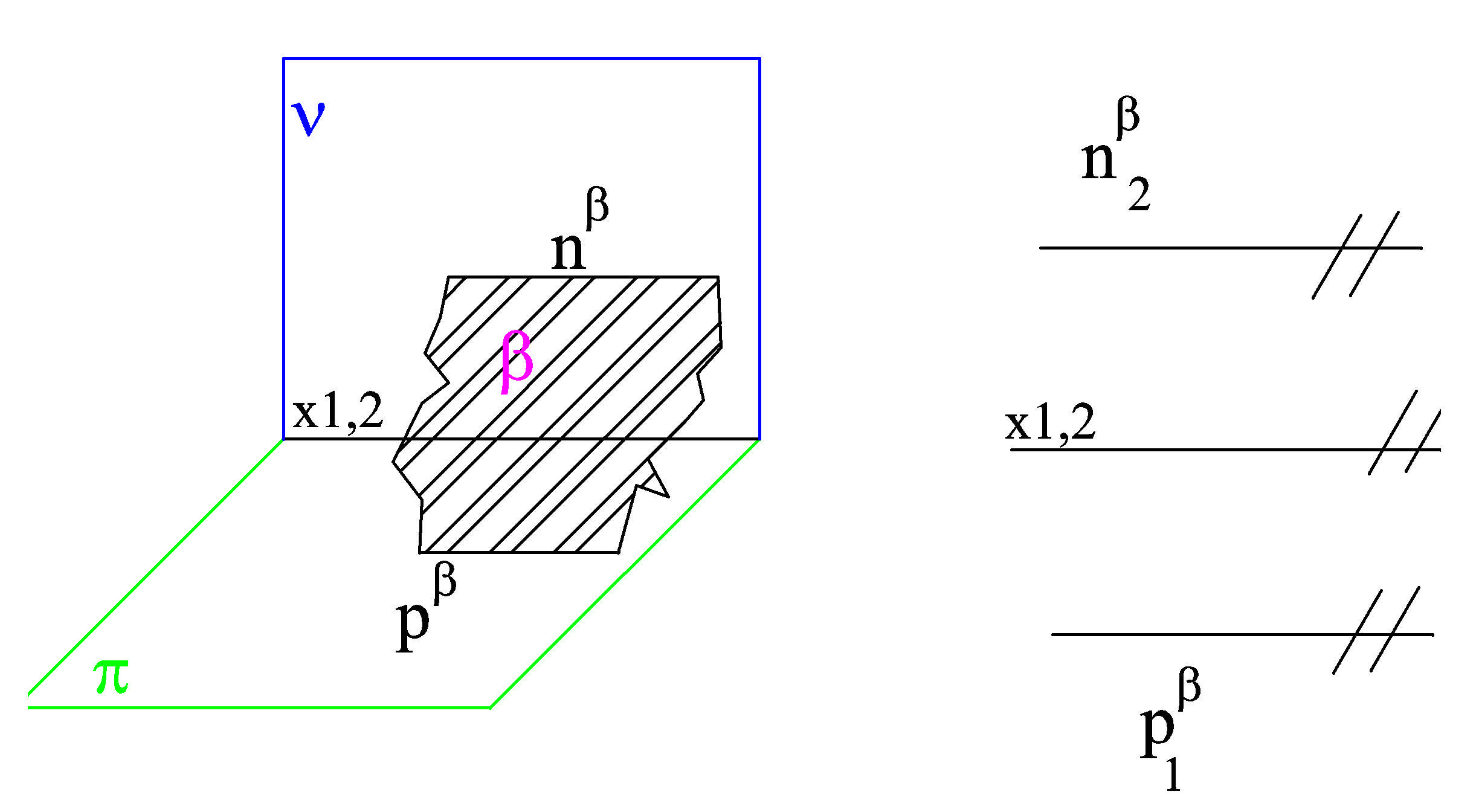
Obr. 6) rovina je různoběžná s oběma průmětnami a rovnoběžná s
y-ovou osou - promítací rovina
- rovnoběžným průmětem roviny rovnoběžné se směrem promítání (promítací rovina) je přímka, rovnoběžným průmětem
jiné roviny je celá průmětna
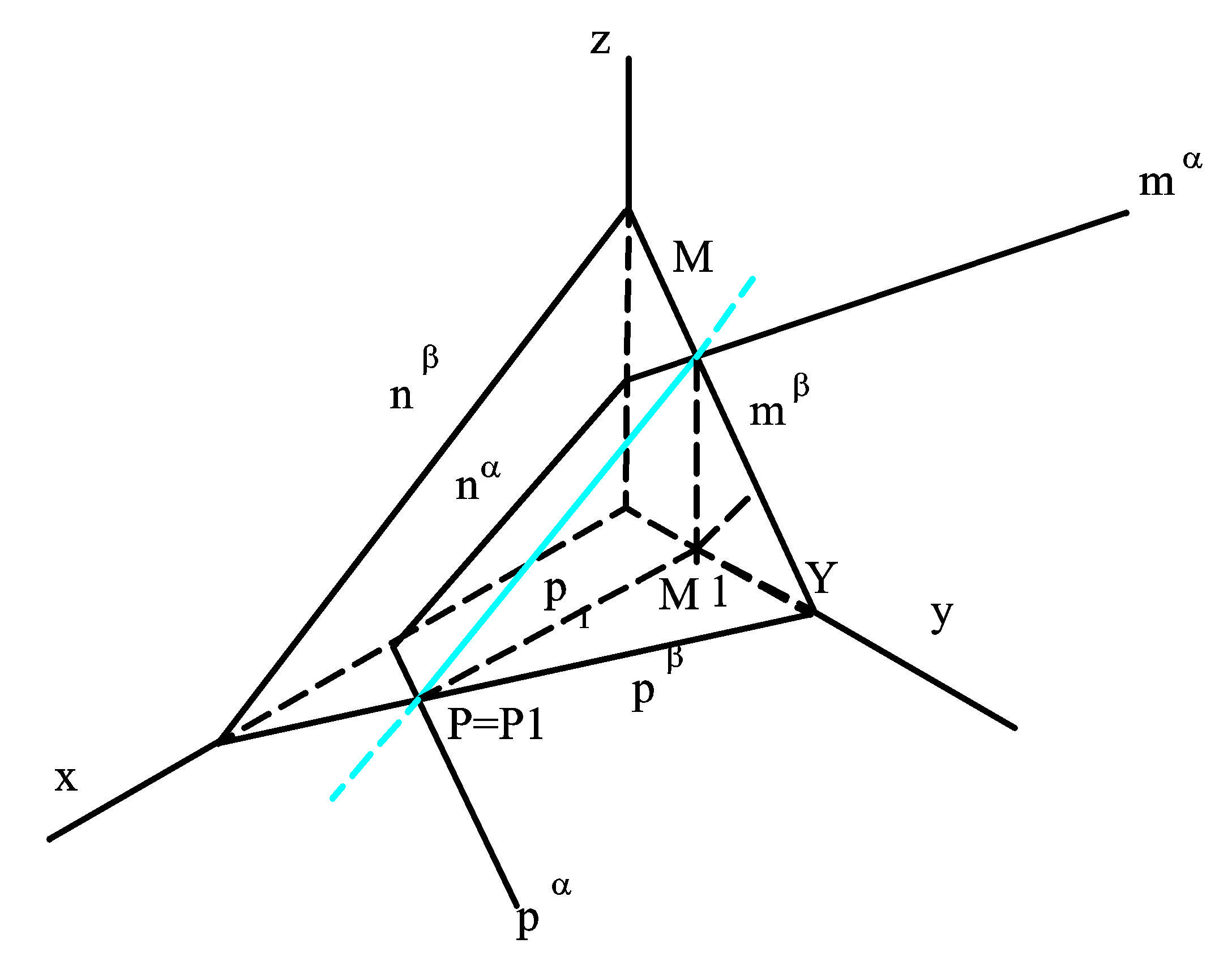
- průsečnice rovin
α | a β | zadaných stopami
- použítí bodů O a P ležící v obou rovinách
- přímka K je průsečnice rovin
- doplnění půdorysu přímky K
Rovinné objekty
Sklápění promítací roviny
Existují dva druhy promítacích rovin:
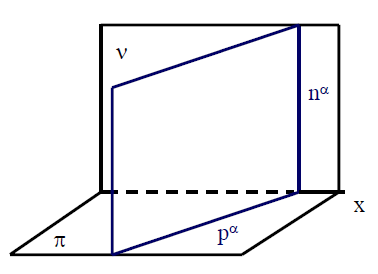
Obr. Půdorysně promítací rovina
α kolmá na
π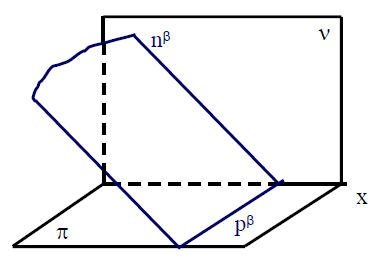
Obr. Nárysně promítací rovina
β kolmá na
νPravoúhlým průmětem útvaru, který neleží v rovině rovnoběžné s průmětnou, je útvar zmenšený
a zkreslený. Pokud chceme znát jeho skutečnou velikost, musíme rovinu otočit do polohy rovnoběžné s průmětnou.
Je-li uvažovaná rovina promítací, otáčíme ji o 90° a mluvíme o sklápění promítací roviny
.
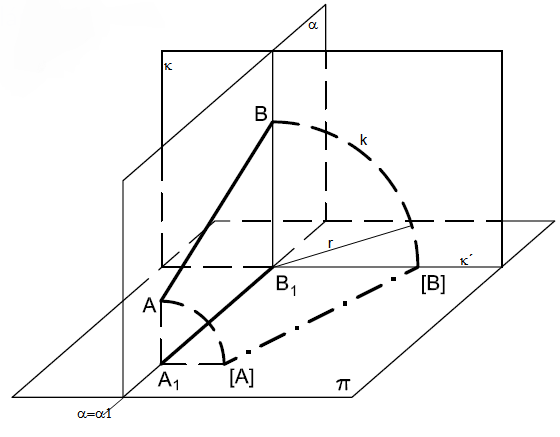
Při sklápění promítací roviny α do průmětny π otáčíme rovinu α kolem osy α 1=α ∩ π .
Libovolný bod B roviny α se otáčí po kružnici k do bodu [B] ∈ π . Protože κ kolmý α' , je κ
kolmý π a κ´ kolmý α´ . [B] ∈ κ a |[B]B´|=|BB´|= poloměr r kružnice k= vzdálenost bodu B od π .
Je-li α promítací rovina úsečky AB, sestrojíme obdobně bod [A]. Sklopenou úsečku [A][B] rýsujeme čerchovaně. Její velikost
je rovna skutečné velikosti úsečky AB.
Zobrazení objektů v promítací rovině
Chceme sestrojit skutečnou velikost rovnostranného trojúhleníka (A)(B)(C)
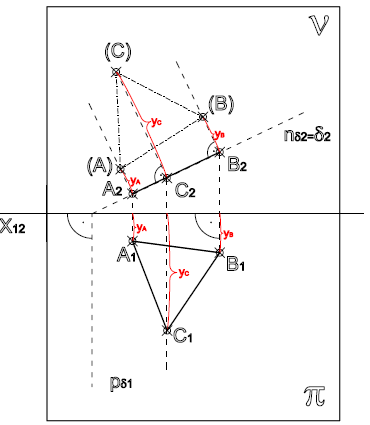
Obr. Skutečná velikost trojúhelníku
Máme zadány souřadnice bodů A1 a B1 v půdorysně π a známe nárysnou stopu roviny δ n δ
2. Sestrojíme body A2 a B2 tak, že spustíme kolmici na osu x z bodu A1 a poté také z bodu B1. Body A2 a B2 nalezneme
na stopě roviny δ . K získání sklopeného bodu (A) musíme vést bodem A2 kolmici na nárysnou stopu roviny δ .
Na kolmici vyneseme y-ovou souřadnici bodu A1. To samé provedeme k získání bodu (B). Získáme úsečku (A)(B) a sestrojíme vrchol (C).
Získali jsme skutečnou velikost rovnostranného trojúhelníku (A)(B)(C). Z bodu (C) vedeme kolmici na nárysnou stopu roviny δ
a na průsečíku kolmice a stopě roviny získáme bod C2. Znovu sestrojíme kolmici, tentokrát na osu x, na kolmici vyneseme vzdálenost
|(C)C2| a získáme bod C1. Můžeme sestrojit trojúhelník A1 B1 C1.
Konstrukci provedeme takto:
Známe body A1, B1 i body A2, B2. Úsečkou A1 B1 vedeme přímku, která je půdorysnou stopou
roviny δ, když přímka narazí na osu x, spustíme na osu x kolmici a dostaneme nárysný stopník roviny δ .
Bodem A1 vedeme kolmici na půdorysnou stopu, na ní vyneseme z-ovou souřadnici bodu A1 a dostaneme
sklopený bod (A). Znovu vedeme kolmici, tentokrát bodem B1, vyneseme z-ovou souřadnici bodu B2
a vznikne sklopený bod (B).
Určení skutečné velikosti úsečky
= nejzákladnější metrická úloha
- úsečka se promítá ve skutečné velikosti v té průmětně, se kterou je rovnoběžná
- úsečka se promítá jako bod v té průmětně, ke které je kolmá
- v Mongeově projekci se velikost úsečky určuje z průmětu (průmět úsečky = dvojice úseček spojujících průměty koncových bodů)
- úsečka v obecné poloze se v pravoúhlém promítání nezobrazuje ve skutečné velikosti
- velikost úsečky se promítáním zkracuje
- skutečná velikost úsečky je (vyjma speciálních poloh) menší, než délky průmetů úsečky
- její skutečnou velikost určíme sklopením první nebo druhé promítací roviny úsečky do
příslušné průmětny => sestrojíme sklopenou polohu promítacího útvaru
- úsečka je v obecné poloze k základnici a průmětnám => k určení skutečné velikosti úsečky z jejího prvního a druhého průmětu
musíme použít konstrukci sklopení nebo otočení úsečky
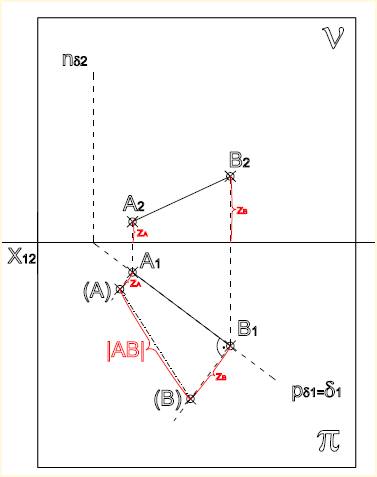
Sklopení úsečky
- sklopíme příslušnou promítací rovinu kolem příslušného průmětu úsečky do půdorysny nebo nárysny (obr. Princip sklopení),
tzn.sklopíme bud její první promítací rovinu do půdorysny, nebo její druhou promítací rovinu do nárysny
1) sklopení úsečky AB do půdorysny: v koncových bodech A1,B1 vztyčíme kolmice k
A1B1 ; na kolmice orientovaně naneseme (do opačných, nebo do stejné poloroviny)
z-ové souřadnice bodu AB
2) sklopení úsečky AB do nárysny: v koncových bodech A2,B2
vztyčíme kolmice k A2B2 ; na kolmice orientovaně naneseme (do opačných, nebo do stejné poloroviny)
y-ové souřadnice bodu AB
- bod A se sklopí do bodu (A) a bod B do bodu (B)
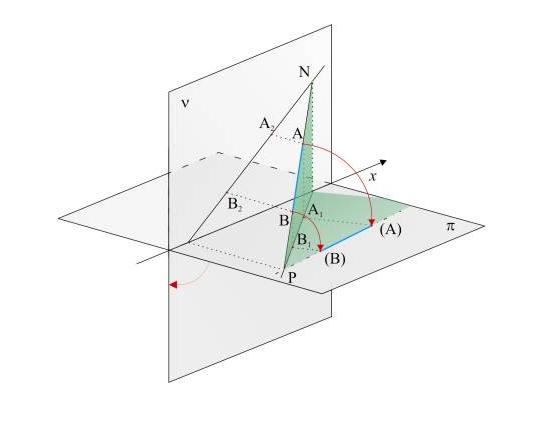
Obr. Princip sklopení [čteme:
A ve sklopení,
B ve sklopení]
Otočení úsečky
- druhou promítací rovinu přímky AB mužeme otočit kolem druhé promítací přímky bodu A do polohy
rovnoběžné s půdorysnou
- druhý rozdílový trojúhelník SAB otočíme kolem své odvěsny SA do polohy rovnoběžné s půdorysnou a skutečná
velikost úsečky AB je velikost úsečky A1OB1
[bod OB1 se nazývá půdorys bodu B v otočení]
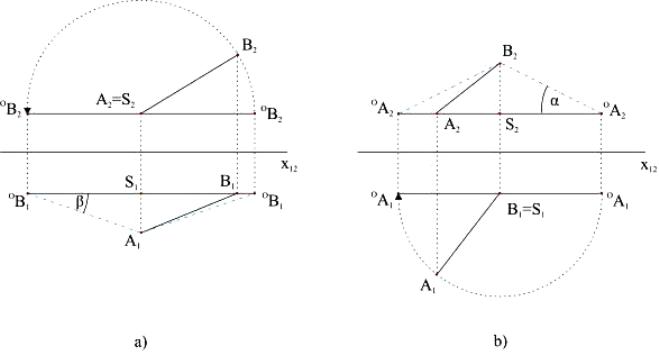
Obr. Určení skutečné velikosti úsečky pomocí otáčení
[ a) otočíme druhý rozdílový trojúhelník do polohy rovnoběžné s půdorysnou ; b) otočíme první rozdílový trojúhelník
do polohy rovnoběžné s nárysnou ]
Speciální polohy přímky
- přímka rovnoběžná s průmětnou => velikost se zachovává
- přímka kolmá k průmětně => promítá se jako bod
- přímka ležící v průmětně => splývá se svým průmětem
- viz. Obr. Speciální polohy přímky
Zobrazení kružnice v promítací rovině
- pravoúhlým průmětem kružnice k = (S, r), jejíž rovina svírá s průmětnou ostrý úhel, je elipsa
- její střed je průmět středu kružnice
- velikost hlavní poloosy elipsy je rovna r
- velikost vedlejší poloosy se určuje graficky
- hlavní osa elipsy leží na hlavní přímce roviny kružnice, protože úsečka, která se zobrazí ve skutečné velikosti,
musí být rovnoběžná s průmětnou; všechny ostatní průměry se zobrazí zkrácené
- toto vše platí jak pro půdorys, tak pro nárys
- sestrojíme sdružené průměty kružnice k = (S, r), která leží v rovině ρ = (1hρ,
2hρ), kde 1hρ ∩ 2hρ = S
- A1, B1 ........... hlavní vrcholy půdorysu kružnice k
- U2, V2 ........... hlavní vrcholy nárysu kružnice k
- A2, B2 náleží 1hρ2
- k sestrojení velikosti vedlejší poloosy nárysu elipsy použijeme např. bod A2
|A2X| = a = r => |A2Y| = b
=> sestrojíme vedlejší vrcholy W2, Z2 a celou elipsu k2
- obdobně postupujeme při konstrukci půdorysu:U1, V1 náleží 2hρ
1 ; |U1X| = a = r => |U1Y| = b
.jpg)
Obr. Zobrazení kružnice
k = (S, r)
- pokud je kružnice dána jinak, např. třemi body nebo středem a tečnou =>
je nejvýhodnější otočit rovinu této kružnice do některé z průměten,
v otočení kružnici sestrojit a poté vrátit zpět do půdorysu a nárysu
- v rovině ρ = (S, t) sestrojíme kružnici k, která je dána středem S a dotýká se přímky t
- rovinu ρ otočíme např. do nárysny kolem hlavní přímky 2.osnovy ležící v nárysně, tj. kolem nárysné stopy roviny
ρ
- při sestrojení jejich sdružených průmětů užijeme toho, že nρ1 = x12
a že průměty hlavních přímek roviny jsou vzájemně rovnobežné přímky
- v otočení sestrojíme kružnici k ve skutečné velikosti k0
- elipsa k2 je afinní, její konstrukce viz. kapitola Afinita
- konstrukce půdorysu k1 se provádí analogicky - v otočení roviny ρ do půdorysny
nebo jako na předchozím obr. Zobrazení kružnice k = (S, r)
.jpg)
Obr. Zobrazení kružnice
k = (S, t )
Sestrojení kolmice k promítací rovině
Def:
Přímka se nazývá kolmá k rovině, je-li kolmá ke všem přímkám této roviny.
Věta:
Přímka je kolmá k rovině ω, je-li kolmá alespoň ke dvěma různoběžným přímkám této roviny.
Víme, že kolmice a k rovině ω je kolmá ke všem přímkám roviny ω a tedy i k hlavním přímkám této roviny. Použijeme-li větu o pravoúhlém průmětu pravého úhlu, dostaneme pro průměty a1, a2 kolmice a k rovině ω
Z bodu A sestrojíme přímku a kolmou ke stopám roviny ω
Obdobným způsobem sestrojíme kolmici i tehdy, jestliže rovina bude zadána pomocí dvou rovnoběžných nebo různoběžných přímek
Ke konstrukci bychom použili hlavní přímky roviny
Zobrazeni těles:
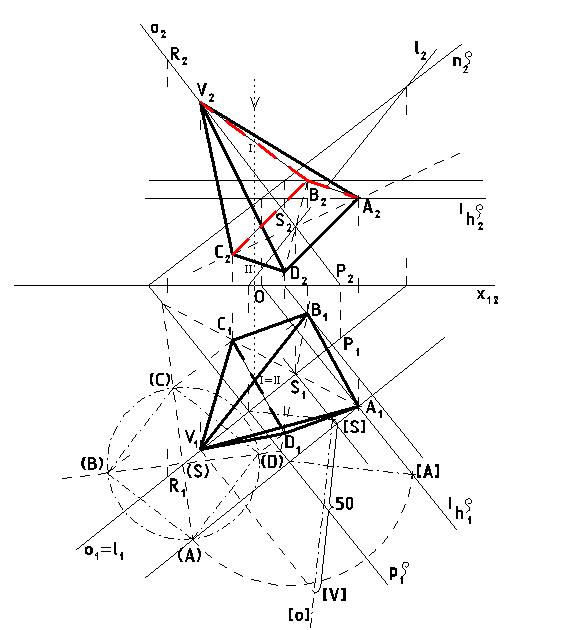
V Mongeově projekci zobrazte pravidelný čtyřboký jehlan ABCDV, je-li dána jeho osa o(P[25, 15, 0], R[-25, 55, 65]), jeden vrchol podstavy A[30, 35, 25] a výška jehlanu v=50. Vrchol V jehlanu leží nad rovinou podstavy
Postupujeme:
1) ρ ; A leží v ρ, ρ je kolmá na o
2) S = o průnik ρ
3) čtverec ABCD, otočením roviny ρ do půdorysny:
a) otočíme bod A do bodu (A),
b) v otočení sestrojíme čtverec (A)(B)(C)(D),
c) afinitou převedeme do půdorysu na rovnoběžník A1B1C1D1,
d) převedeme do nárysu na ordinálách a pomocí hlavních přímek na rovnoběžník A2B2C2D2,
4) V ; V leží na o, |SV| = 50mm, yV > yS, zV > zS.
5) Viditelnost jehlanu v půdoryse: Obrysové hrany jehlanu budou určitě viditelné, tzn. že můžeme rovnou plně vytáhnout pětiúhelník A1B1C1V1D1.
I. způsob:
V prostoru nám tyto hrany obrysu rozdělí jehlan na dvě části, viditelnou a neviditelnou. Hrany AV a BV leží v jedné části a hrana CD v druhé, tzn. že hrany AV a BV budou mít stejnou viditelnost a hrana CD opačnou. Stačí tedy určit viditelnost jedné dvojice hran, například BV a CD. Ty jsou v prostoru mimoběžné, takže jejich viditelnost v půdoryse určíme pomocí jejich zdánlivého průsečíku I=II. V půdoryse budou viditelné hrany AV a BV a neviditelné bude hrana CD.
II. způsob:
Vrcholy a hrany jehlanu ležící na obrysu jsou vždy viditelné. Stačí určit viditelnost hran ležících uvnitř obrysu, tj. hran AV, BV a CD. Viditelnost v půdorysu určujeme z nárysu (při pohledu shora). Porovnáním z-ových souřadnic vrcholu V jehlanu a středu S podstavy zjistíme, zda leží výš vrchol V nebo střed S a s ním i celá podstava. Vrchol V má větší z-ovou souřadnici než bod S, proto leží výš něž podstava jehlanu. Tzn. že podstava je při pohledu shora zakrytá jehlanem a hrana CD je v půdorysu neviditelná. Hrany AV, BV mají vzhledem k ostatním hranám jehlanu největší z-ové souřadnice a jsou proto v půdorysu viditelné.
6) Viditelnost jehlanu v náryse: Nejprve plně vytáhneme obrysové hrany, tzn. čtyřúhelník A2V2C2D2.
I. způsob:
Ten nám opět v prostoru rozdělí jehlan na dvě části. Hrany AB, BC, BV leží v jedné části (budou mít stejnou viditelnost) a hrana DV v druhé (bude mít viditelnost opačnou). Pomocí zdánlivého průsečíků hran BC a DV zjistíme, že hrana DV je v náryse viditelná a hrany AB, BC, BV jsou v náryse neviditelné.
II. způsob:
Vrcholy a hrany jehlanu ležící na obrysu jsou viditelné. Určíme viditelnost vrcholů a hran ležících uvnitř obrysu. Viditelnost v nárysu určujeme z půdorysu (při pohledu zepředu). Porovnáním y-ových souřadnic vrcholu V jehlanu a středu S podstavy zjistíme, zda leží vpředu vrchol V nebo střed S a s ním celá podstava. Větší y-ovou souřadnici má bod V, leží tedy před podstavou jehlanu, která je při pohledu zepředu jehlanem zakrytá. Všechny hrany vedoucí z neviditelných vrcholů jsou neviditelné. Protože vrchol B podstavy je v nárysu neviditelný, musí být v nárysu neviditelné i hrany AB, BC a BV. Hrana DV má vzhledem k ostatním hranám největší y-ové souřadnice a je v nárysu viditelná.
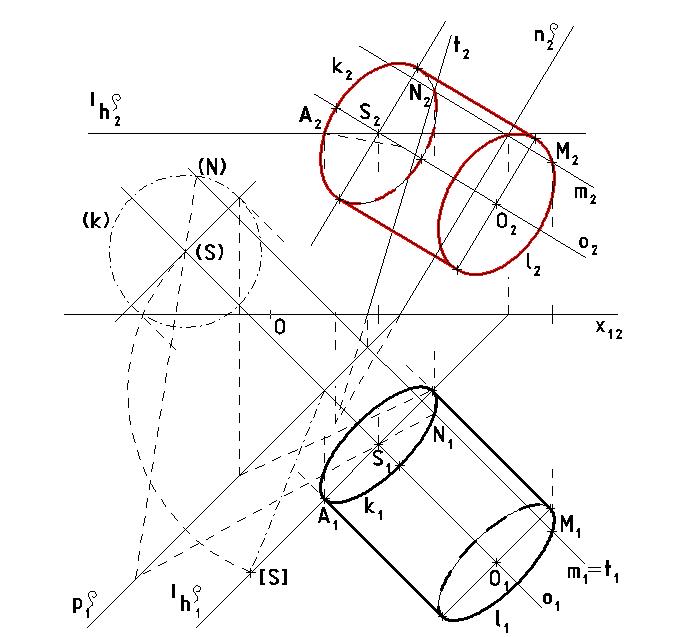
Sestrojte rotační válec ψ s podstavou k v rovině ρ(30, 30, -50), je-li dán střed S[25, 30, ?] podstavy k a bod M[65, 50, 35], který leží na kružnici druhé podstavy l.
Pomocí hlavní přímky první osnovy sestrojíme nárys bodu S. Bodem M vedeme kolmici m k rovině ρ. Její průsečík s rovinou ρ je bod N. Otočíme body S a N kolem půdorysné stopy do půdorysny. V otočení sestrojíme kružnici (k) a afinitou převedeme na půdorys k1. Hlavní osa nárysu k2 leží na hlavní přímce druhé osnovy a vedlejší osu omezíme pomocí proužkové konstrukce sestrojené v bodě A2. Osa o je kolmá k rovině ρ a prochází středem S. Protože se shodné rovnoběžné úsečky promítají stejně dlouhé, platí |M1N1|=|O1S1| a |M2N2|=|O2S2|. Hlavní a vedlejší osa elipsy l1 jsou stejně velké jako hlavní a vedlejší osa elipsy k1. Protože podstavy k a l leží v rovinách rovnoběžných, musí být navíc hlavní osy spolu rovnoběžné. Obdobně pro nárys l2.
Viditelnost:
Protože zS>zO, leží střed S a s ním i podstava k vzhledem k půdorysně výše a je tedy v půdorysu celá viditelná. Dále yO>yS , podstava l proto leží vzhledem k nárysně více vpředu než podstava k a je v nárysu celá viditelná.
Shrnutí:
Při konstrukci těles využíváme základní úlohy. Před konstrukcí tělesa ze zadaných prvků provádíme zpravidla rozbor řešení, ve kterém hledáme vztahy zadaných prvků a prvků, které umožní bezprostřední konstrukci tělesa.
U těles s podstavou v půdorysně využíváme toho, že se podstava zobrazí do půdorysu ve skutečné velikosti a do nárys jako úsečka. U těchto těles se základní úlohy většinou redukují na speciální případy úseček, přímek a rovin.
Viditelnost těles určujeme pomocí jejich obrysu. Obrys rozdělí těleso na dvě části, viditelnou a neviditelnou. Hrany na viditelné části jsou viditelné (rýsujeme plně), hrany na neviditelné části jsou neviditelné (rýsujeme čárkovaně).
U hranolu a válce porovnáním z-ových, resp.y-ových souřadnic středů podstav určíme, která podstava leží výše, resp. vpředu. Podstava ležící výše, resp. vpředu je v půdorysu, resp. v nárysu, viditelná. Druhá podstava je neviditelná.
U jehlanu a kužele porovnáním z-ových, resp.y-ových souřadnic středu podstavy a vrcholu jehlanu (kužele) zjistíme, zda leží výše, resp. vpředu, podstava nebo vrchol jehlanu (kužele). Leží-li vrchol výš než podstava, resp. před podstavou, je podstava v půdorysu, resp. v nárysu, neviditelná. V opačném případě je viditelná.
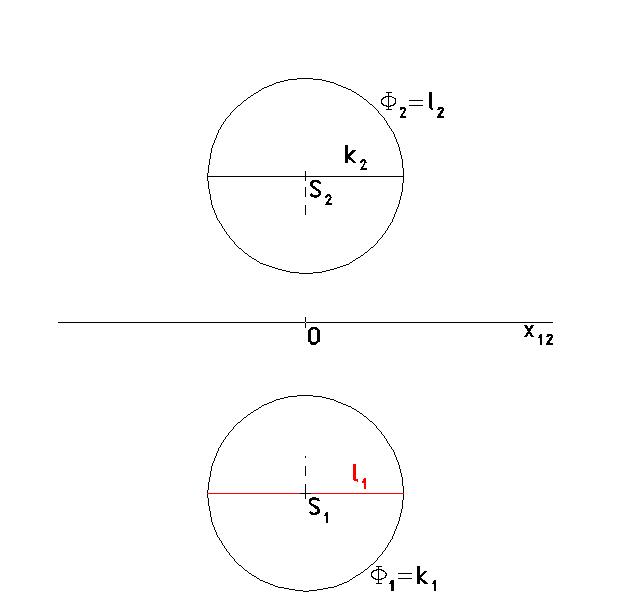
Zobrazení rovnoběžkových kružnic a poledníků na kulové ploše.
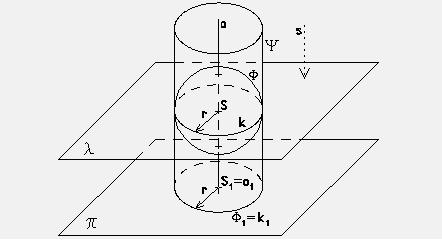
Kulová plocha Φ je množina všech bodů prostoru, které mají od pevného vlastního bodu S, zvaného střed kulové plochy, tutéž vzdálenost r, kterou nazýváme poloměr kulové plochy. Značíme Φ (S, r).
Průměty kulové plochy
Nejprve rozebereme kolmý průmět kulové plochy Φ do půdorysny π. Jestliže každým bodem kulové plochy vedeme promítací přímku rovnoběžnou se směrem promítání s, vyplní všechny tyto promítací přímky rotační válec ψ. Jeho osa o je kolmá k půdorysně a poloměr r je roven poloměru kulové plochy. Půdorys kulové plochy je průnik tohoto válce s půdorysnou, což je kruh Φ1(S1, r).
Průmětem obrysové kružnice k kulové plochy je v půdorysu kružnice k1(S1, r). Kružnice k leží v prostoru na kulové ploše a v rovině l, která je rovnoběžná s půdorysnou a jde středem S. Kružnice k určuje viditelnost kulové plochy v půdorysu: Body ležící na kulové ploše nad kružnicí k budou v půdorysu viditelné, body ležící na kulové ploše pod kružnicí k budou v půdorysu neviditelné.
Předchozí úvaha se týkala kolmého průmětu kulové plochy do půdorysny. Analogicky tedy kolmým průmětem kulové plochy do nárysny musí být kruh Φ2(S2, r). Nárysným obrysem pak musí být kružnice l, která leží v rovině rovnoběžné s nárysnou.
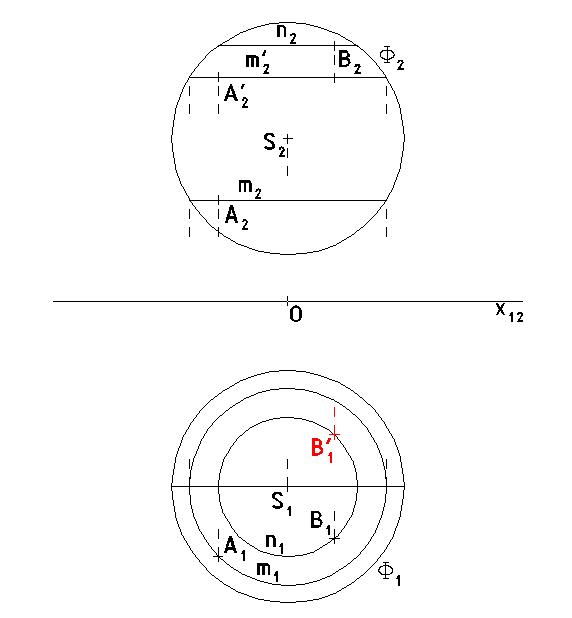
Sestrojte průměty kulové plochy Φ(S[0, 35, 30], r=20). Určete oba průměty kružnic k, l, které tvoří obrys kulové plochy v půdorysu a v nárysu.
Řešení:
Půdorysem kulové plochy je kruh Φ1(S1, r=20), nárysem je kruh Φ2 (S2, r=20). Obrysová kružnice v půdorysu je kružnice k1, které splyne s hranicí kruhu Φ1. Kružnice k leží v rovině rovnoběžné s půdorysnou a jdoucí středem S. Jejím nárysem je úsečka k2, která prochází středem S2, je rovnoběžná se základnicí a tvoří průměr kruhu Φ2. Obdobně obrysová kružnice v nárysu je kružnice l2, které splyne s hranicí kruhu Φ2. Kružnice l leží v rovině rovnoběžné s nárysnou a jdoucí středem S. Jejím půdorysem je úsečka l1, která prochází středem S1, je rovnoběžná se základnicí a tvoří průměr kruhu Φ1.
Na kulové ploše Φ(S[0, 40, 35], r=25) jsou dány body A[-15, 55, ?], B[10, ?, 55]. Sestrojte chybějící průměty bodů A a B, jestliže platí zA< zS, yB> yS (tzn. že z-ová souřadnice bodu A je menší než z-ová souřadnice bodu S a y-ová souřadnice bodu B je větší než y-ová souřadnice bodu S).
Jestliže bodem A vedeme rovinu rovnoběžnou s půdorysnou, řeže tato rovina kulovou plochu Φ v kružnici m, jejímž půdorysem je kružnice m1 se středem S1 a jdoucí bodem A1. Nárysem kružnice m je úsečka m2, která má velikost průměru kružnice m a která tvoří tětivu kružnice Φ2 rovnoběžnou se základnicí. Bod A2 odvodíme na ordinále. Ze dvou řešení A2 a A'2 vybereme A2, neboť splňuje zadanou podmínku. Půdorys bodu B sestrojíme pomocí kružnice n. Její poloměr odečteme z nárysu a bod B1 odvodíme na ordinále. Ze dvou řešení B1 a B'1 vybereme B1, neboť splňuje zadanou podmínku.
Literatura
- Rádl, P.: Konstruktivní geometrie, Mendelova zemědělská a lesnícká univerzita v Brně, 2000.
- Setzer, O. - Kula, K.: Deskriptivní geometrie, Praha, 1979.
- Švercl, J.: Zobrazovací metody, Praha 1971.
- Borecká, K.-Chvalinová, L. a kol.: KONSTRUKTIVNÍ GEOMETRIE. Akademické nakladatelství CERM, s.r.o., Brno, 2002.
- Kargerová, M. - Mertl, P.: Geometrie, skripta Fakulty dopravní ČVUT, 1997.
- Doležal, M.: Základy deskriptivní a konstruktivní geometrie díl 3., Mongeovo promítání, VŠB - Technická univerzita Ostrava, 2006.
Odkazy
- http://mat.fsv.cvut.cz/BAKALARI/kog/files/DEG_Svetlana.pdf
- http://www.gymberoun.cz/~hamernik/dg/
- http://mdg.vsb.cz/jdolezal/Deskriptiva/Prednaska/Monge/Uvod.html
- http://www.deskriptivnigeometrie.ic.cz/mongeovoprom.php
- http://www.fp.vslib.cz/kmd/lide/bimova/FS/FS-KGE910_01predn.ppt/
- http://mat.fsv.cvut.cz/krivkova/obrazkyKOG/3.prednaska09naweb.pps















.jpg)
.jpg)