Deskriptivní geometrie je věda o zobrazení prostorových útvarů do roviny (průmětny). Podstatou deskriptivní geometrie je jednoznačný vztah mezi zobrazovaným objektem a jeho průmětem (jedním nebo více). Zjednodušeně řečeno jde o zobrazování trojrozměrných útvarů na dvojrozměrnou nákresnu. Nejzákladnější objekty, se kterými pracuje, jsou body, přímky, roviny a úhly. Praktické využití našla deskriptivní geometrie všude tam, kde je třeba technicky přesně zakreslit různé prostorové útvary (strojírenství, architektura…).
Počátky deskriptivní geometrie úzce souvisí s počátky stavebnictví. Stavby, které měly být postaveny, bylo totiž nutné předem vyrýsovat do kamene. Proto bylo nutné nalézt způsob zobrazení trojrozměrných útvarů na dvojrozměrný prostor. Zároveň však mělo být umožněno na obrazech útvarů provádění jistých planimetrických konstrukcí tak, aby získané výsledky bylo možno opět přenášet zpět na útvary v prostoru. Lineární promítací metody byly používány již v Chaldeji (2300 př.n.l.) a starém Egyptě (1200 př.n.l.). Jednalo se v podstatě o pravoúhlé promítání na jednu průmětnu. Toto promítání, které se blíží svým pojetím dnešnímu kótovanému promítání, bylo použito při stavbách pyramid, akvaduktů, chrámů, průplavů, silnic a dalších.
Za zakladatele deskriptivní geometrie v dnešním slova smyslu je považován Gaspard Monge (1746-1818), který v díle Géometrie descriptive (1799) popsal kolmé promítání na dvě kolmé průmětny. Dříve rozptýlené a na empirismu založené metody sjednotil a na jednoduchých geometrických základech založil novou promítací soustavu, nazvanou po něm Mongeovo promítání. Nastává velmi prudký rozvoj této vědní disciplíny v celé střední Evropě.
Další vývoj zobrazovacích metod si vyžádal vývoj malířství. Pro správné provedení malby zobrazovaného předmětu se začala od 15. století používat lineární perspektiva. Jejími průkopníky byli např. Fillippo Brunelleschi a Leon Battista Alberti. Teprve poté dochází k rozvoji rovnoběžného promítání, a to nejdříve kosoúhlého. To bylo využíváno především ve vojenství, a to hlavně k zobrazování celých měst nebo jejich významných částí.
Plány a projekty stavebních objektů a technických předmětů jsou zpravidla kresleny v kolmém promítání na sdružené průmětny, takzvanou půdorysnu, nárysnu a bokorysnu, z nichž se dají snadno číst rozměry objektů, podle kterých zkušený odborník dovede plán posoudit a projekt uskutečnit. Ale i sebezkušenějšímu znalci nebývá vždy při složitých objektech zběžným nahlédnutím do takto kresleného rysu patrný celkový vzhled objektu, jak by se mu jevil při přímém pozorování. Že bychom si velmi těžko učinili skutečnou a správnou představu i o zcela jednoduchých útvarech ze dvou sdružených průmětů kolmých například z půdorysu a nárysu, kde jsou zobrazeny dva útvary poměrně velmi jednoduché, nebo z nárysu a bokorysu, který představuje čtyřboký hranol ze dvou různých dřev sestavený, anebo dokonce nebudeme moudří ani z obrázku, v němž jsou narýsovány vedle sebe tři základní geometrické útvary jako půdorys, nárys a bokorys zcela jednoduchého tělesa.
Snažíme se tedy zobrazit útvar i tak, že předložený obraz vyvolá v každém, i na necvičeném oku, dojem, jaký by vyvolal samotný originál. Jednou takovou zobrazovací metodou je kosoúhlé promítání, někdy také nazývané rovnoběžnou perspektivou.
Kolmé promítání není názorné proto, že zobrazované útvary spočívají obyčejně svými podstavnými stěnami právě v rovinách, na něž kolmo promítáme, a hrany a stěny kolmé k těmto podstavám se pak zobrazují jako body a úsečky. Abychom zobrazili hrany opět jako úsečky a obrazce jako obrazce, promítáme je paprsky rovnoběžnými, ale takovými, že svírají s průmětnou, na které je zachytíme, kosý úhel. Směr těchto paprsků musí být tedy napřed určen.
Při pozorování (čtení) takového kosoúhlého průmětu si však musíme uvědomit, že zrakový dojem jím vyvolaný se bude tím více shodovat s dojmem skutečným, čím méně se bude odchylka zrakových paprsků s průmětnou lišit od odchylky paprsků promítacích, které promítaly dané těleso. Pozorujeme tedy tyto obrazy z větší vzdálenosti a nestavíme je přímo před sebe jako průměty pravoúhlé, ale stranou. Kosoúhlé průměty útvarů budou především sloužit názornému zobrazení objektu. Budou zpravidla sestrojovány jako doplněk pravoúhlých průmětů. Můžeme však v tomto promítání zobrazovat i řešení geometrických úloh prostorových, úloh polohových, které se zakládají jen na spojování, protínání a rovnoběžnosti základních geometrických útvarů, bodů, přímek a rovin nebo úloh metrických, to je úloh o velikosti úseček, úhlů, vzdáleností a podobně.
Chci-li konstruovat nějaký bod, nebo úsečku, nebo nějaký jiný libovolný geometrický útvar v kosoúhlém promítání, nutně k tomu potřebuji několik důležitých údajů. Jedním z nich je zadání konkrétního geometrického útvaru, to zde ale teď řešit nechci, to uľ znáte z jiných částí geometrie. Dalším a daleko důleľitějąím údajem je pro kosoúhlé promítání úhel zkosení. Abychom se mohli bavit o úhlu zkosení, potřebujeme nejdříve osový kříž.
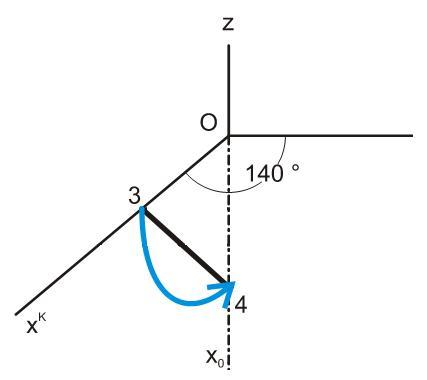
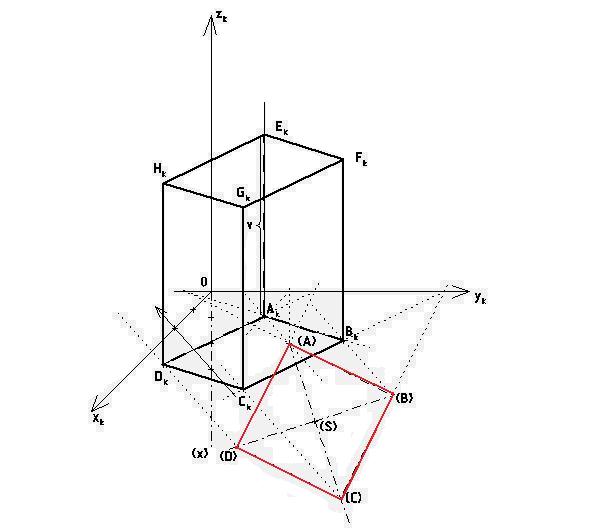
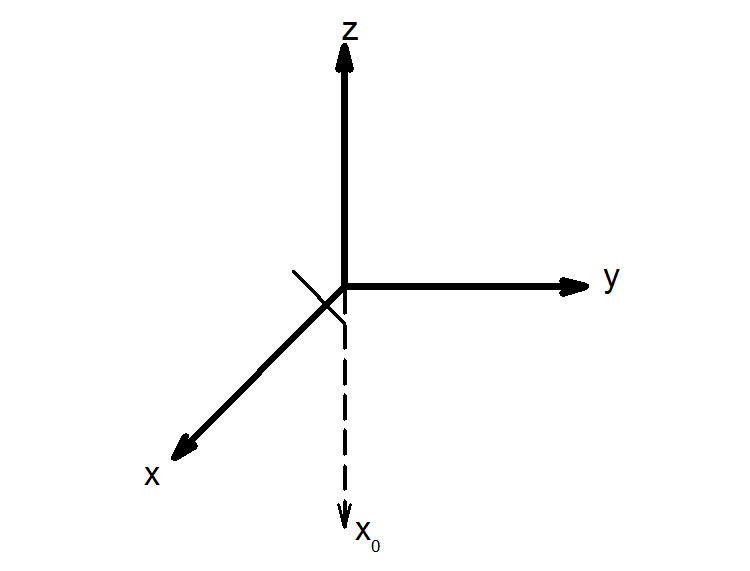
Narýsovat osový kříž umí snad každý z nás, rýsovali jsme ho již hodně krát. V kosoúhlém promítání se užívá kříž, který má osy pojmenované trochu jinak, než-li jsme zvyklí. Vodorovná osa se označuje jako osa y, osa k ní kolmá, tzn. osa svislá je osa z. Osa z je to ale jen pro I. a II. kvadrant. Prodloužení osy z do III. a IV. kvadrantu už se v kosoúhlém promítání nazývá osa x0. A konečně osa xK, osa xK svírá s osou y úhel, který je povětąinou zadán v zadání úlohy a nazývá se úhlem zkosení. Tato osa x prochází IV. kvadrantem. A proč zde máme 2 osy x, akorát jedna je označená jako xK a druhá jako x0? Dozvíte se za chvíli.
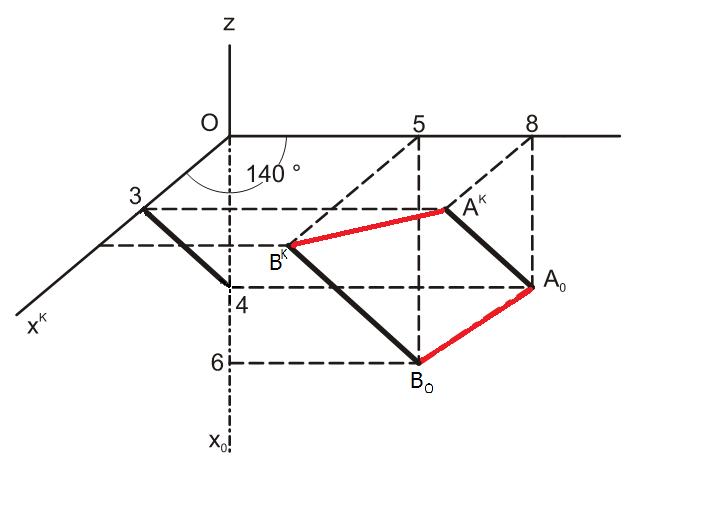
Další důležitou částí zadání je kvocient (q), nebo-li také zkrácení. Tento údaj je nejčastěji zadán pomocí zlomku, například q= 34. Tento kvocient je zadán jako poměr zkrácené jednotky ku skutečné jednotce. V našem případě je skutečná část rovna 4 jednotkám a zkrácená část je rovna 3 jednotkám. Teď si vysvětlíme, jak tento fakt zakomponovat do nám již známého osového kříže pro kosoúhlé promítání. A nyní jsme u toho, proč máme 2 různé osy označené jako xk a x0. Na osu x0 vyneseme jmenovatel zlomku kvocientu, v našem případě 4 jednotky. Na osu x Knaneseme čitatel zlomku, v našem případě 3 jednotky. Kdyľ spojíme tytodva vzniklé body, tak dostaneme směr Anfinity.
Vysvětlíme, jak tento fakt zakomponovat do nám již známého osového kříže pro kosoúhlé promítání. A nyní jsme u toho, proč máme 2 různé osy označené jako
Afinita - Mezi kosoúhlými průměty bodů v půdorysně a otočenými průměty těchto bodů je afinní vztah. Afinita je geometrické zobrazení, při kterém odpovídají rovnoběžným přímkám opět rovnoběžné přímky, které však nemusí být rovnoběžné s původními přímkami. Osa afinity je zde totožná s osou y.
Obrázek:

Osa y, vodorovná osa v rovině µ
Osa z kolmá na osu y
Osa xk, která svírá s osou y úhel &omega, který je vždy zadán v zadání úlohy
Osa x0, která je prodloužením osy y do roviny &pi
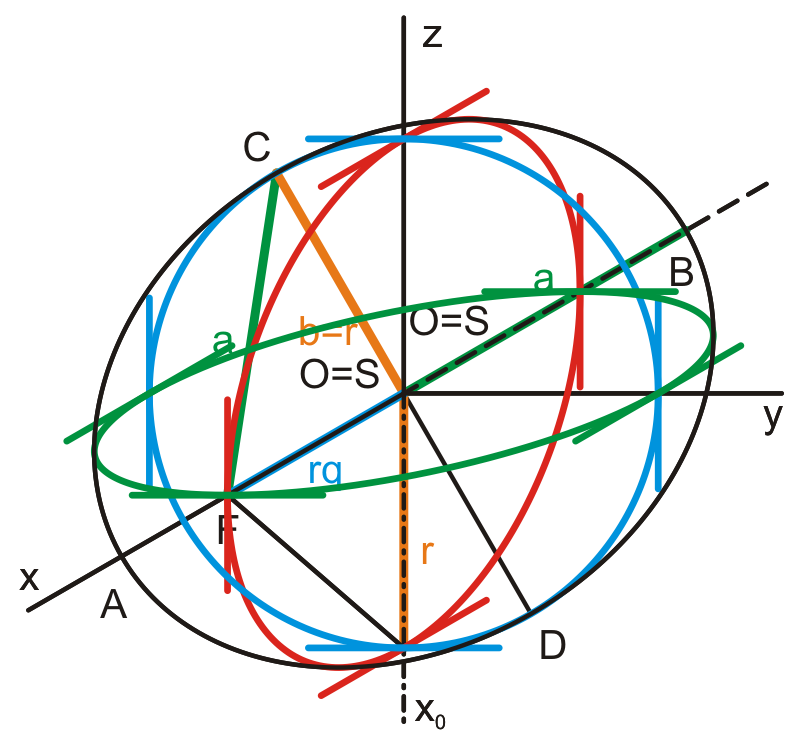
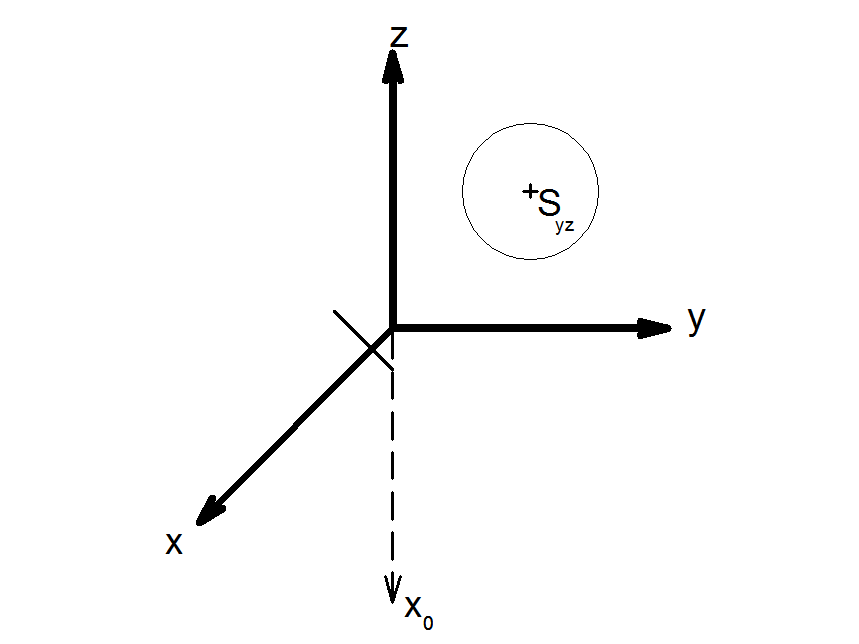
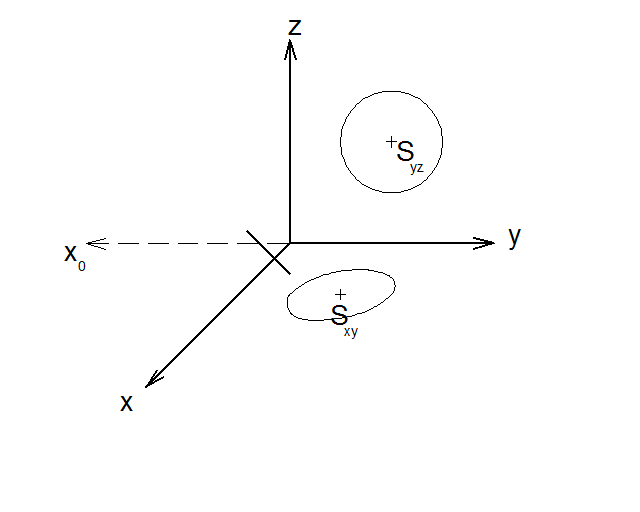
Př. Zobrazte kružnice ve všech promítacích rovinách kosoúhlého promítání. Poloměry kružnic r = 5,
Sxy [10, 10, 0], Sxz [10,0,10], Syz [0,10,10]. Promítání proveďte pro q =12, &omega =135°.
1) narýsujeme si souřadné osy a směr zkrácení
2) jako první narýsujeme kružnici v rovině yz, protože je to nejjednodušší a nedochází zde ke zkracování, případně ke zkreslování. Tudíž vyneseme souřadnice středu a na osách y a z a narýsujeme kružnici o poloměru 5.
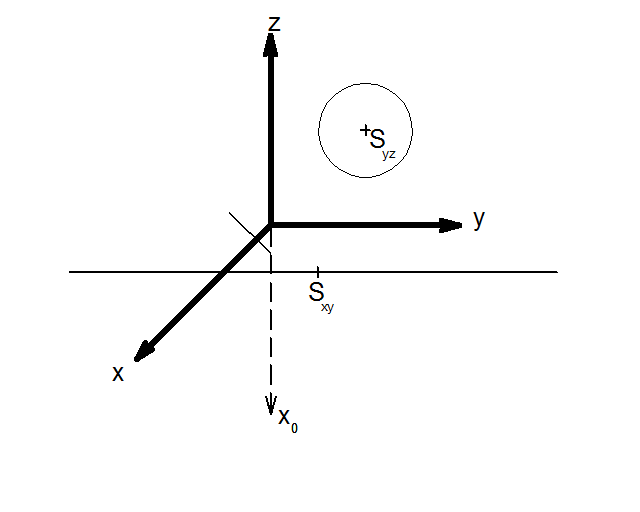
3) Nyní narýsujeme kružnici v rovině xy. Nejprve musíme zobrazit střed Sxy [10, 10, 0] a to tak, že nejprve na pomocné ose x0 vyneseme x-ovou souřadnici Sxy (10) a na ose y vyneseme y-novou souřadnici. Vznikne nám střed S0 . Následně pak sestrojíme jeho obraz, dle pravidel kosoúhlého promítání.
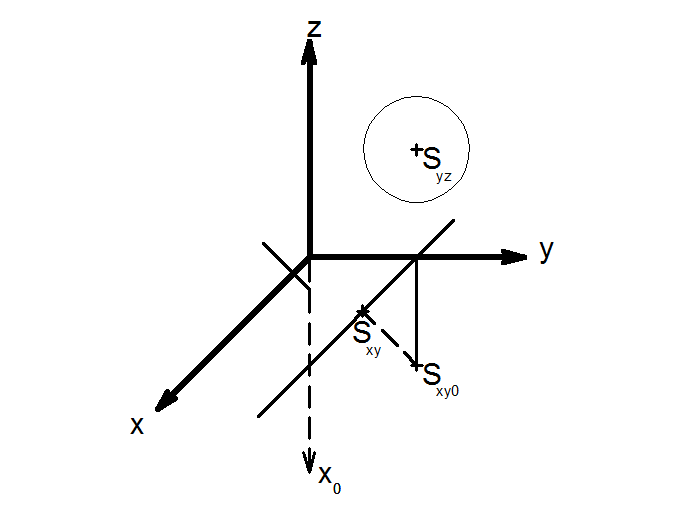
4) Pro zobrazení kružnice si musíme uvědomit pár věcí. Obrazem kružnice bude elipsa, jejíž hlavní poloosa bude ležet na přímce, která bude rovnoběžná s osou y a bude procházet středem Sxy .
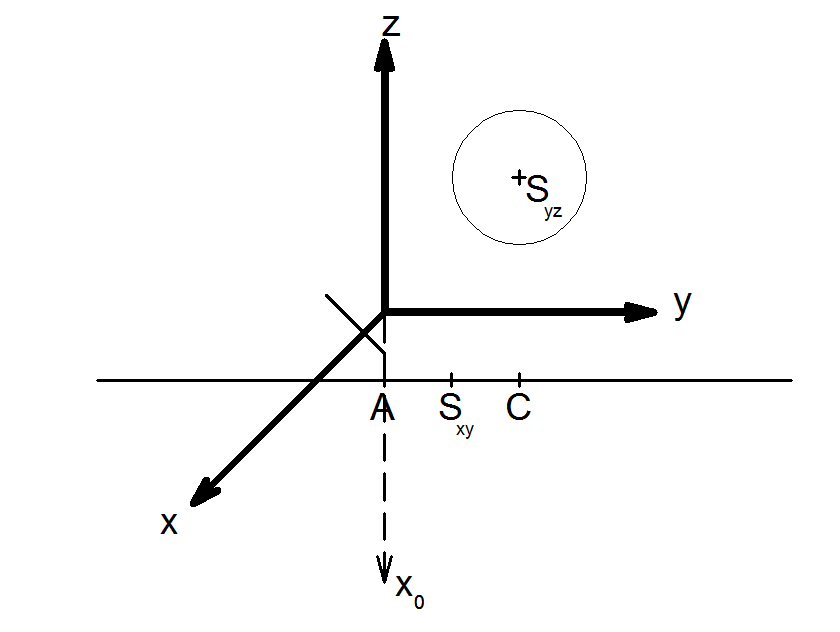
5) Velikost hlavní poloosy bude rovna poloměru zobrazované kružnice, protože ve směru osy y nedochází ke zkracování. Vynesením vzdálenosti 5 od bodu Sxy, který je středem elipsy, získáme krajní body elipsy A a C.
6) Poloosa b bude ležet na přímce, procházející Sxy a rovnoběžnou s osou x. Její velikost ovšem bude hodnota zkreslených 5. Tuto hodnotu naneseme na přímku, na níž bude ležet poloosa b. Získáme body B a D elipsy.
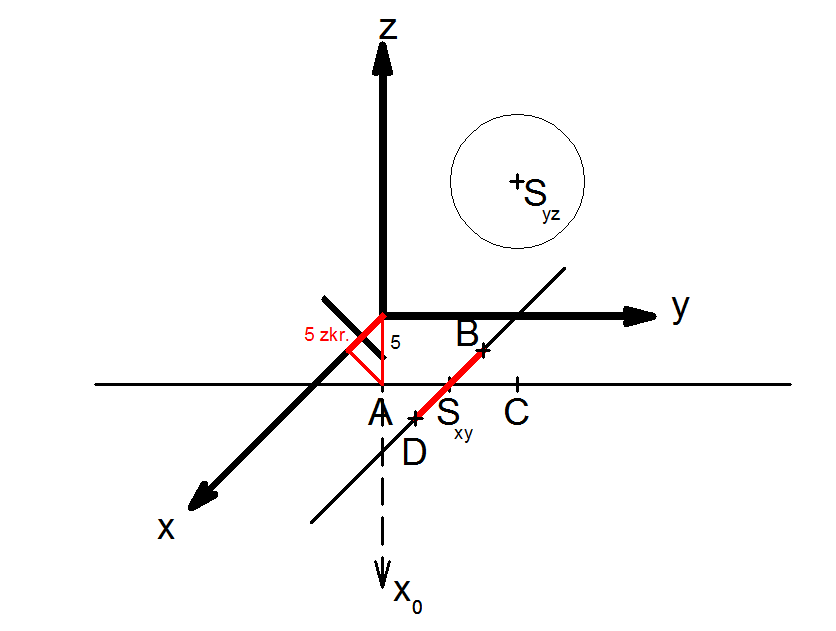
7) Body A a C budeme vést rovnoběžky s osou x a body B a D rovnoběžky osou y, které se protnou a vytvoří tak kosodélník, v němž bude vepsaný obraz kružnice (elipsa).
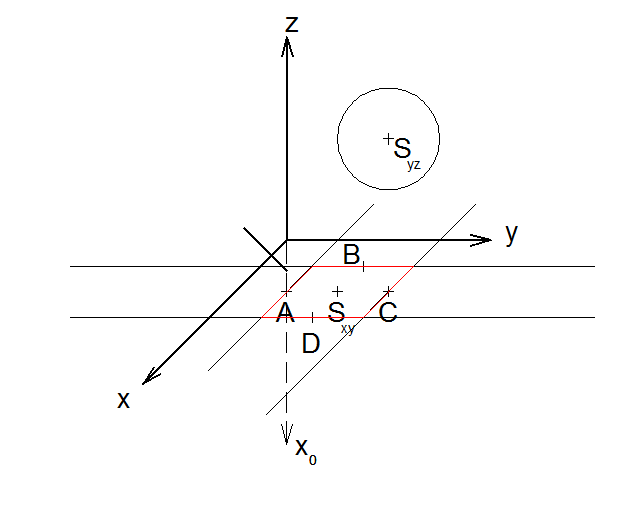
8) Vepíšeme do kosodélníku elipsu tak, aby se dotýkala kosodélníku v bodech A, B, C a D. Tímto získáme obraz kružnice v rovině xy
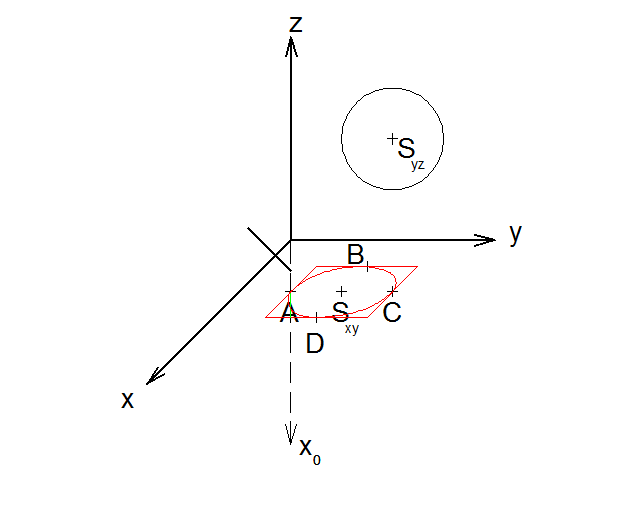
9) Obraz kružnice v rovině xz se sestrojuje analogicky, jako obraz v rovině xy. Nejdříve si ale musíme sestrojit novou pomocnou osu x0, která bude kolmá k ose z. A to kvůli vynášení souřadnic středu a jejich zkreslení právě při zobrazování. Tato osa nám poslouží ke konsrtukci nového směru zkrácení, který může být jiný než v případě roviny xy.
10 ) Jak už jsme zmínili, tak celý postup bude analogický jako v předchozím případě. Jako první tedy sestrojíme obraz středu Sxz.
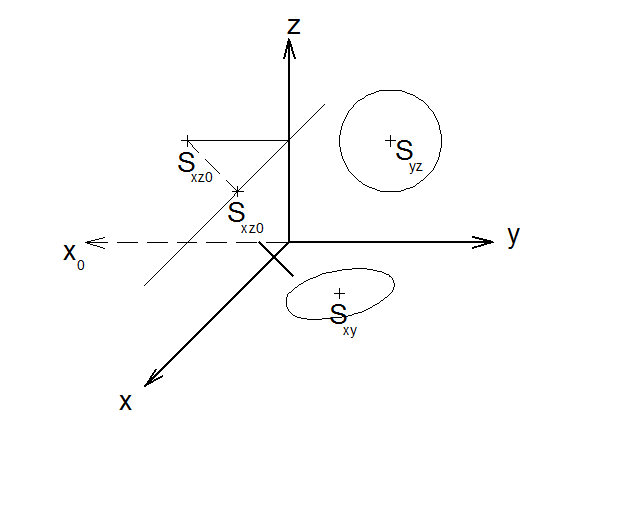
11) Dále sestrojíme hlavní poloosy elipsy, ale POZOR! Nyní zůstane nezkreslená poloosa b, takže sestojíme rovnoběžku s osou z, která prochází bodem Sxz, vyneseme na ni na každou stranu od Sxz vzdálenost 5 a získáme body B a D.
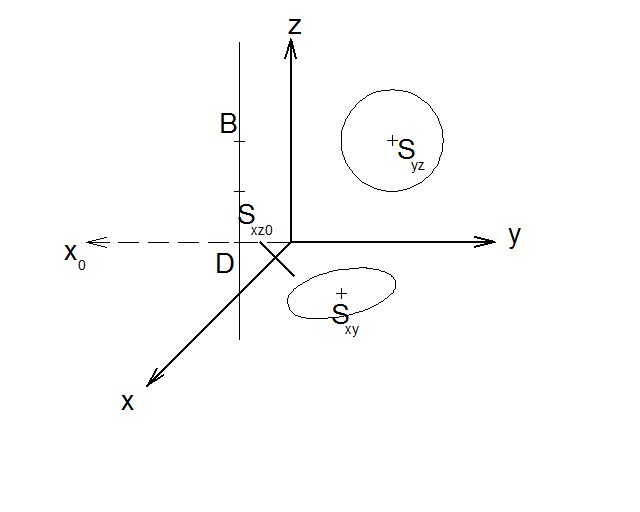
12) Bodem Sxz vedeme rovnoběžku s osou x, zde bude ležet poloosa a. Její délka bude hodnota zkrácených 5. Vynesením této délky získáme body A a C.
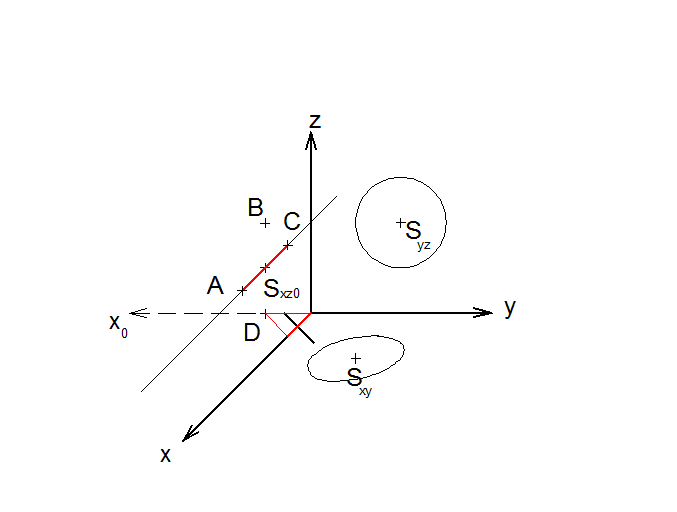
13) Vytvoříme kosodélník, který bude opsaný obrazu kružnice. A vepíšeme mu elipsu za stejných podmínek jako v minulém případě.
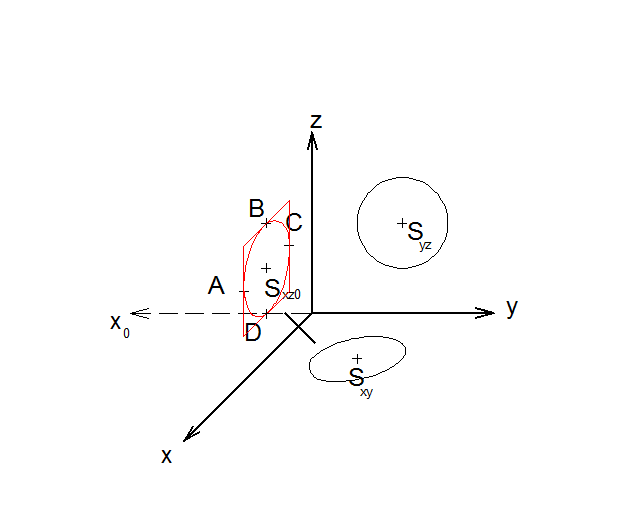
14) Sestrojili jsme tedy obrazy kružnic ve třech souřadných rovinách xy, xz a zy. Jak jsme se přesvědčili, tak v rovinách xy a xz obrazem kružnice jsou elipsy.
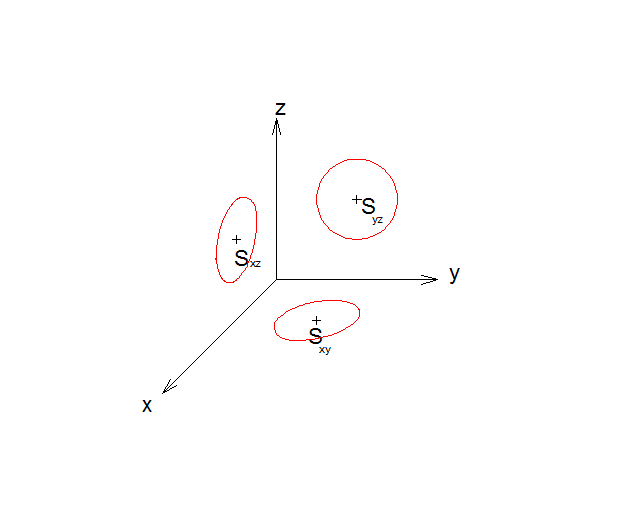
Obrazu kružnic se využívá při tvorbě kulové plochy, kdy se střed koule umístí do počátku osového kříže a zobrazí se všechny výše uvedené obrazy s tímto společným středem. Na závěr se pak obtáhne tento obraz elipsou.