Obr. 1 - Zobrazení bodu
Každá promítací metoda má z pohledu praxe určité výhody i nevýhody podle toho, co při jejím užití vyžadujeme. Protože u kótovaného promítání jde o zobrazení prostoru na jednu rovinu, má toto promítání své uplatnění především ve stavebním inženýrství, v horním inženýrství, a v geologicko-průzkumné praxi při řešení praktických úloh na topografických plochách.
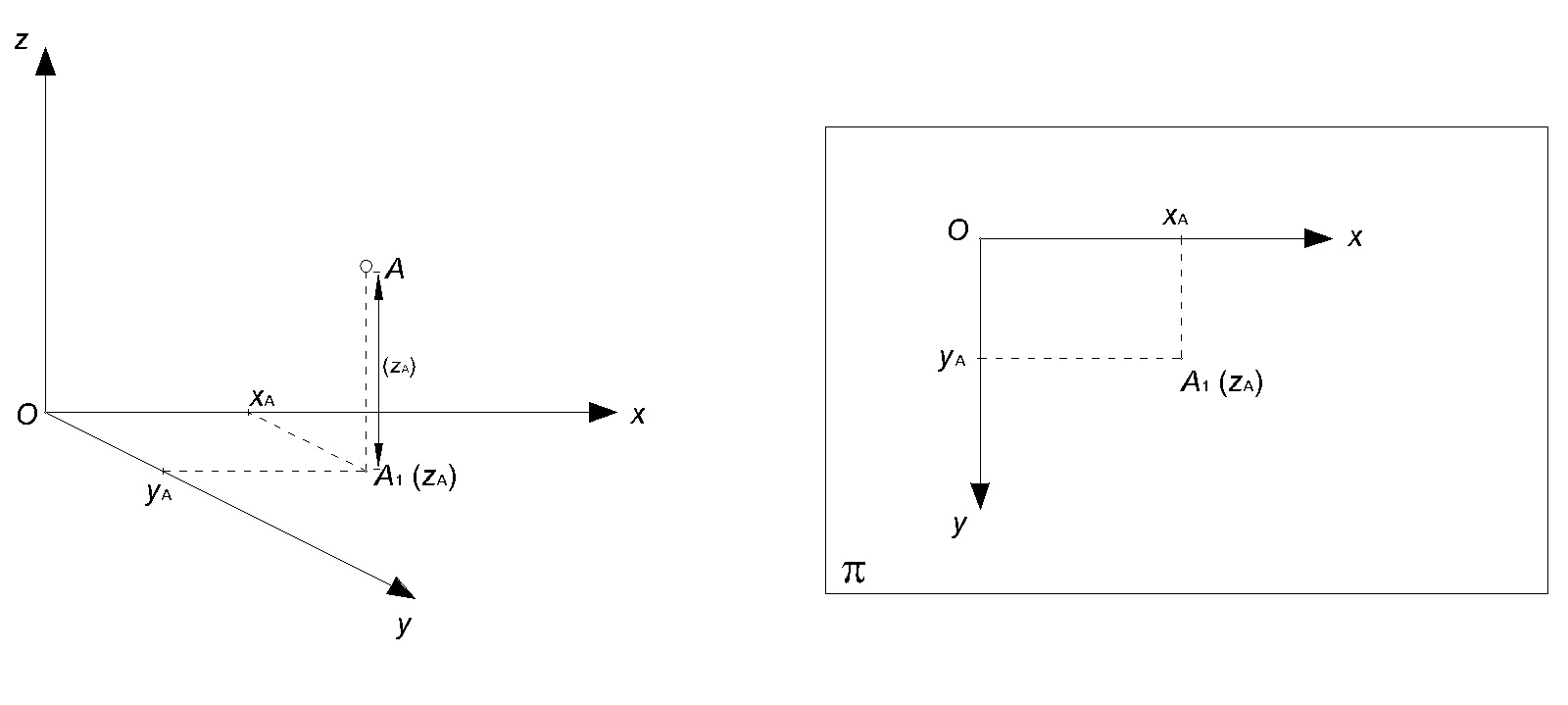
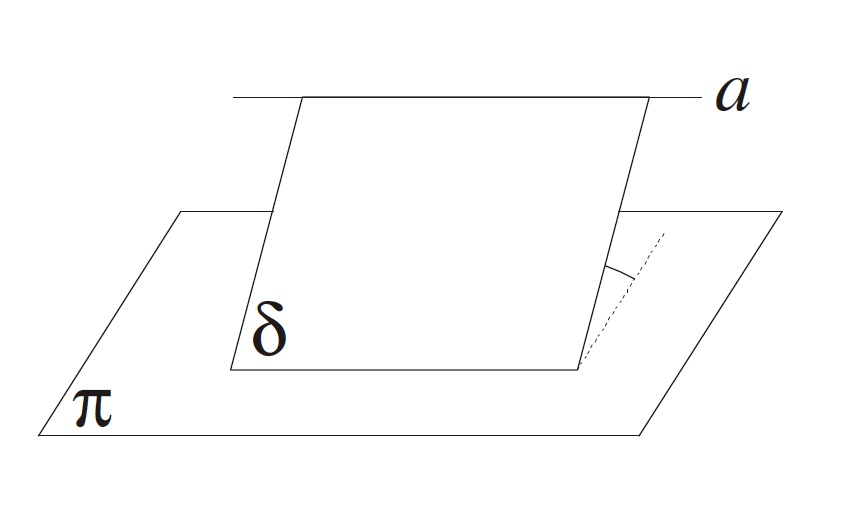
Kótované promítání je rovnoběžné pravoúhlé promítaní na jednu rovinu, kterou nazýváme průmětnou, a označíme ji π. Bod A prostoru zobrazíme tak, že tímto bodem proložíme přímku kolmou k průmětně, kterou nazveme promítací přímkou, a její průsečík A1 s průmětnou π je průmětem bodu A.
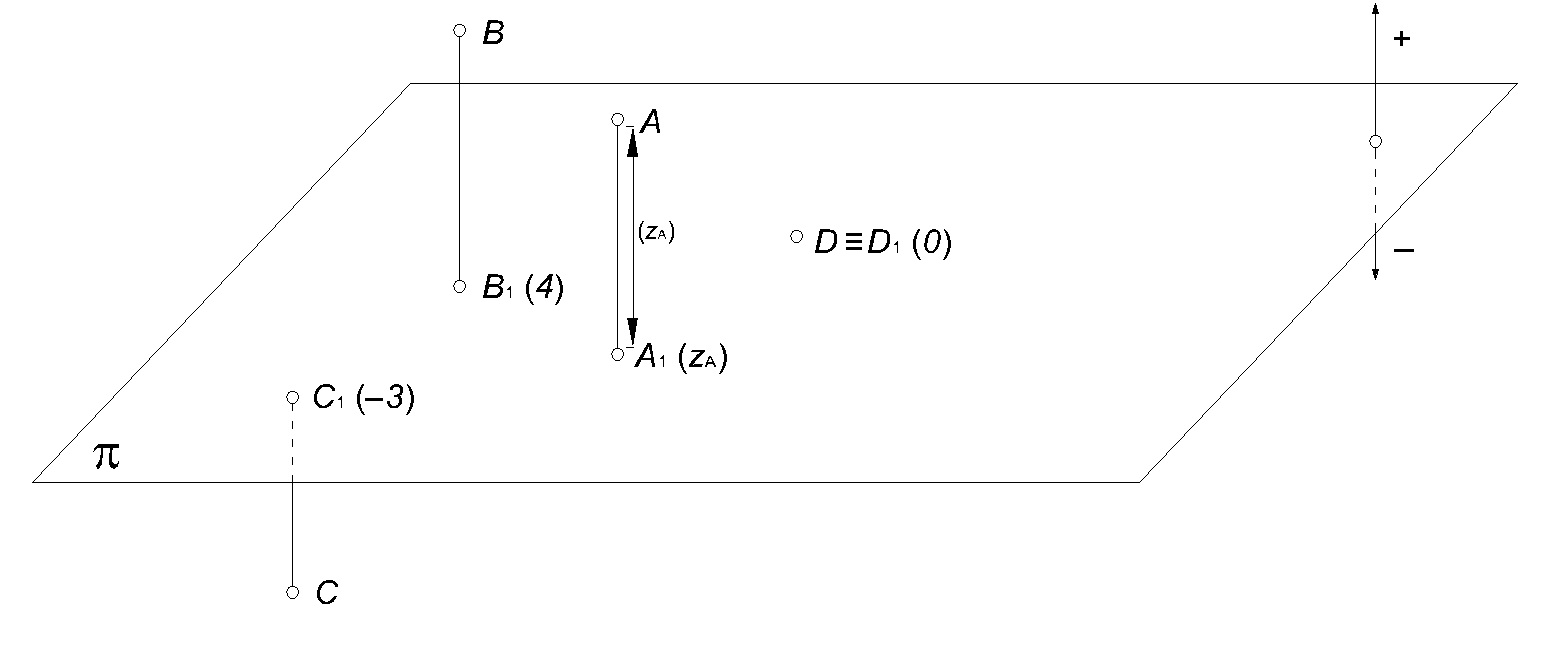
Obrazem A1 není ovšem jeho vzor A v prostoru jednoznačně určen. Abychom dosáhli jednoznačnosti také v opačném směru, užijeme tzv. kóty takto: Průmětna π dělí prostor na dva poloprostory. Jeden označíme za kladný a druhý za záporný. Vzdálenost A1A bodu A od průmětny π bude mít kladné (záporné) znaménko, jestliže bod A bude ležet v kladném (záporném) poloprostoru; leží-li bod A v průmětně, jeho vzdálenost je 0; (obr. 1).

Vzdálenost A1A se znaménkem označíme zA. Je tedy zA orientovaná vzdálenost A1A bodu A od průmětny π.
Orientovaná vzdálenost A1A = zA se nazývá kóta bodu A. Kótu zA připisujeme k průmětu A1 do závorky; píšeme A1(zA).
Pravoúhlý průmět bodu A s kótou nazýváme kótovaný průmět bodu A.
Z kótovaného průmětu A1(zA) můžeme jednoznačně určit jeho vzor A v prostoru. V bodě A1 sestrojíme kolmici, na ni naneseme orientovanou vzdálenost zA a tím dostáváme vzor A obrazu A1(zA).
Kótované promítání je vzájemné jednoznačné zobrazení bodů prostoru do kótovaných průmětů v průmětně. Na obr. 1 a 2 jsou znázorněny v kótovaném promítání body A1(zA), B1(4), C1(-3), D1(0).
V pravoúhlém souřadnicovém systému {0;x;y;z} volíme souřadnicovou rovinu (xy) za průmětnou π kótovaného promítání a kladný poloprostor bude obsahovat kladnou část osy z.
Kótovaný obraz A1(zA) bodu A[xA, yA, zA]sestrojíme tak, že v souřadnicovém systému {0;x;y} v průmětně π sestrojíme bod A1 o souřadnicích xA, yA a jako kótu připíšeme jeho zetovou souřadnici zA. Pro vynášení souřadnic budeme užívat levotočivý souřadnicový systém.
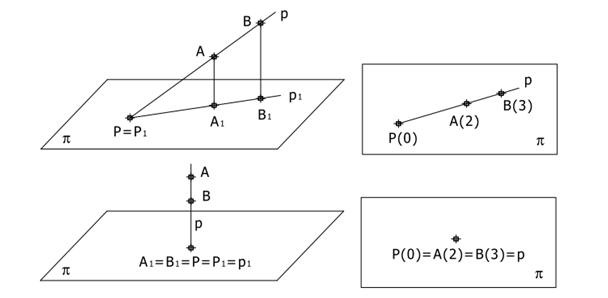
Při zobrazování přímky v kótovaném promítání stačí znát kótované průměty dvou různých bodů přímky. Pravoúhlý průmět p1 přímky p, určené body A a B, je spojnice A1B1, když A1 ≠ B1. V případě, že A1 = B1, pak p1 = A1 = B1, což nastane právě tehdy, když přímka p je kolmá k promítací rovině.
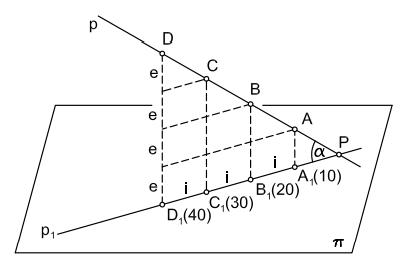
i - interval přímky p
e - ekvidistance
α - odchylka přímky p od průmětny
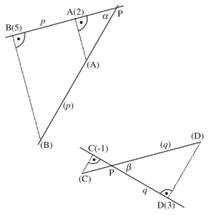
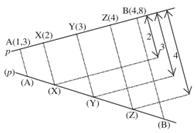
Určete skutečnou velikost úseček AB a CD, stopník přímek p = AB a q = CD a odchylku těchto přímek od průmětny.
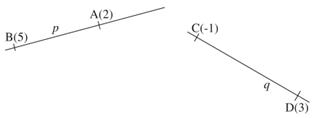
Řešíme pomocí sklápění. V bodech A a B vztyčíme kolmice k přímce p. Z bodu A naneseme na kolmici kótu bodu A a dostáváme sklopený bod (A). Tímto postupem zkonstruujeme i bod (B). Kóty obou bodů mají stejné znaménko, sklopené body tedy musí ležet ve stejné polorovině s hraniční přímkou p. Body (A) a (B) určují sklopenou přímku (p). Skutečná velikost úsečky AB je rovna velikosti úsečky (A)(B). Průnikem přímek p a (p) je hledaný stopník P, odchylka těchto přímek je rovna odchylce přímky p od průmětny. V případě přímky q mají kóty bodů C, D různá znaménka, sklopené body tedy musí ležet v opačných polorovinách s hraniční přímkou q.
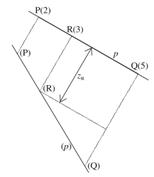
Najděte na přímce p = PQ bod R, který má kótu z R = 3.
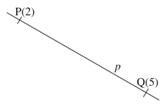
Řešíme opět pomocí sklápění. Sklopíme body P a Q a na přímce (p) najdeme bod, jehož vzdálenost od p je 3. To je bod (R). Z tohoto bodu spustíme kolmici na p a bod, ve kterém tato kolmice protne p, je hledaný bod R.
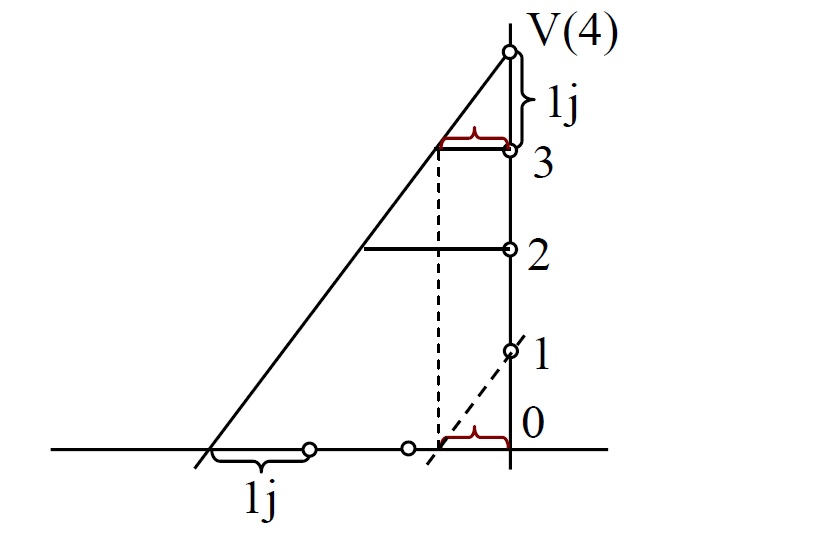
Vystupňujte přímku p = AB.

Řešíme obdobně jako úlohu 2. Na sklopené přímce (p) najdeme body, jejichž vzdálenost od p je 2, 3 a 4, a po kolmici je odvodíme na p.
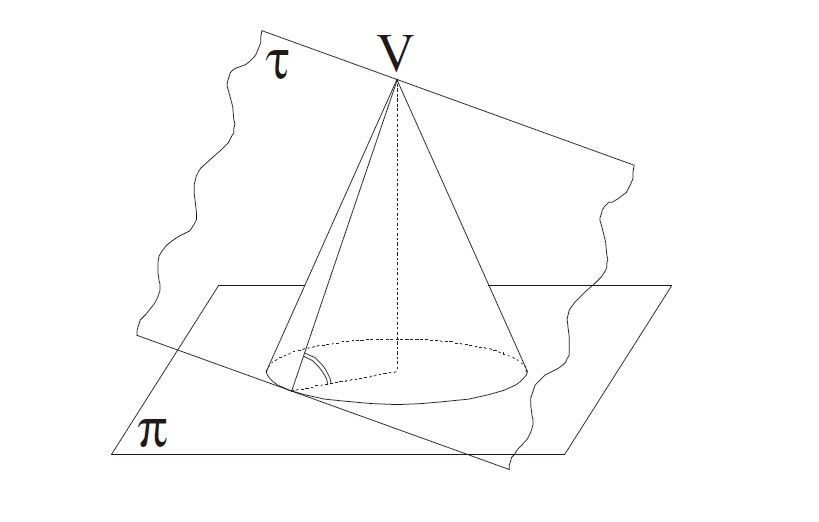
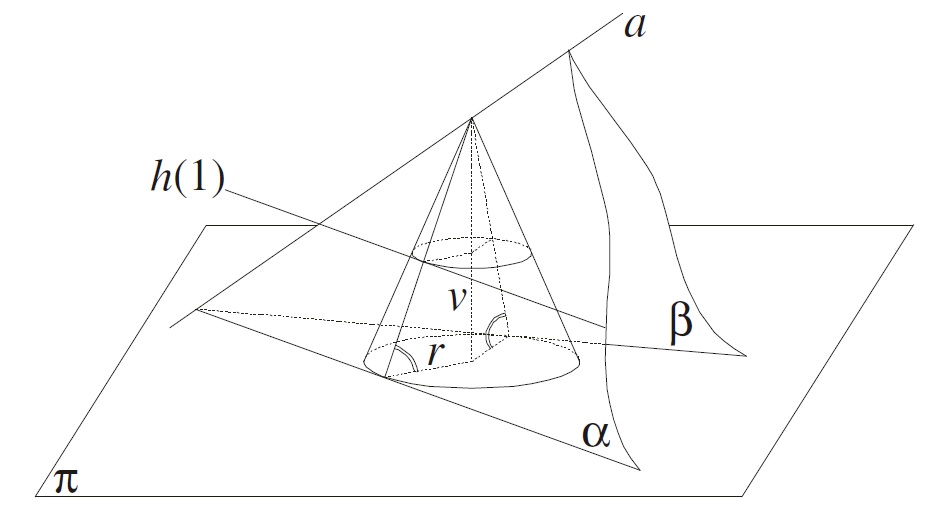
Spádová plocha je plocha, jejíž tečné roviny mají týž spád, tedy jsou rovnoběžné s tečnými rovinami spádového kužele. Spádový kužel je množina přímek, které mají stejnou odchylku od průmětny a procházejí týmž bodem V.
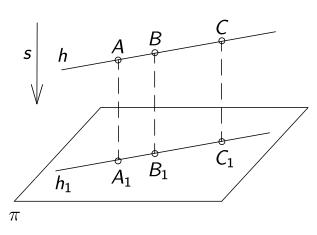
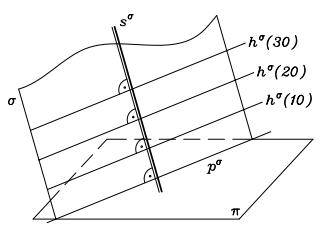
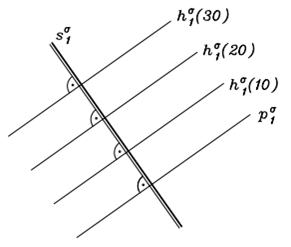
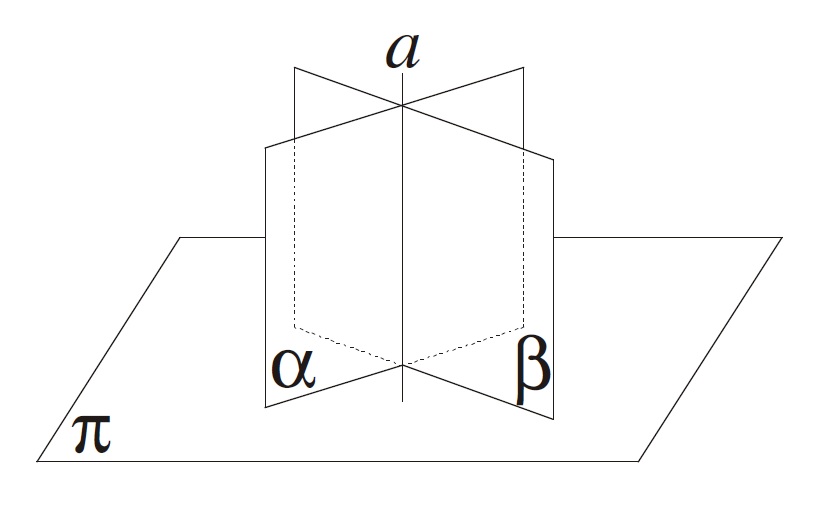
Rovinu α, která není rovnoběžná s průmětnou π, protínají ekvidistantní roviny v horizontálních přímkách h. Takové přímky nazýváme hlavní přímky roviny. Hlavní přímky jsou jejími vrstevnicemi, tj. množinami bodů, které mají stejné kóty. Hlavní přímka p roviny α s nulovou kótou se nazyvá stopa roviny α.
Na obrázku 18. můžeme vidět osový řez spádového kužele.
Spád roviny α je spád její libovolné spádové přímky s. Hledáme-li rovinu α daného spádu s α = tg φ, která prochází bodem V, sestrojíme spádový kužel s vrcholem V. Rovina α je tečnou rovinou plochy spádového kužele. Společná přímka s roviny α a spádového kužele je spádová přímka roviny α.
Tečné roviny spádového kužele prochází vrcholem a mají od průmětny stejnou odchylku jako površky spádového kuželu.
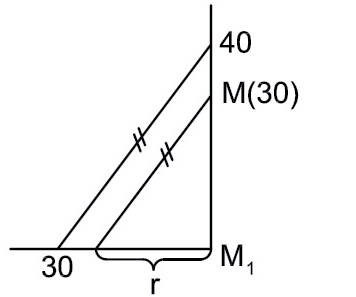
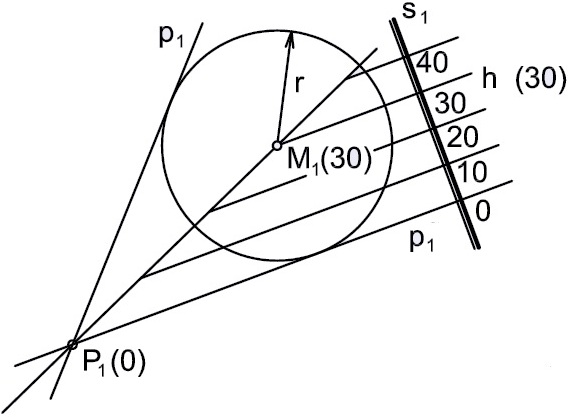
Přímkou PM proložte rovinu o spádu 4/3.
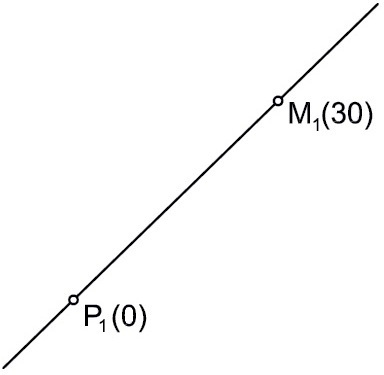
Najdeme úhel odpovídající spádu 4/3. Nejdeme poloměr r podstavy spádového kužele (obr. 23). Vezmeme přímku PM. Sestrojíme podstavu spádového kužele jako kružnici k(M,r). Stopy hledaných rovin jsou tečny ke kružnici k z bodu P. Pro rovinu α sestrojíme spádovou přímku S1. Hlavní přímka h(30) roviny α prochází bodem M. Vystupňujeme spádovou přímku a sestrojíme další hlavní přímky. Výsledné přímky nám dávají rovinu o spádu 4/3 procházející přímkou PM (obr. 24).