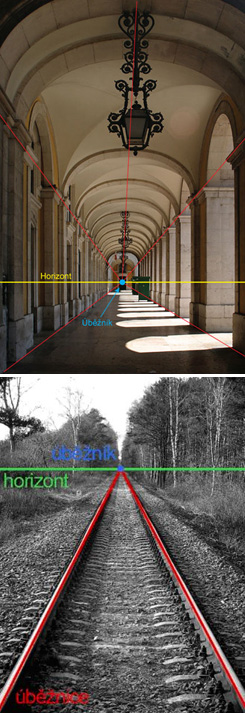
Obr. 1 - sbíhající se kolejnice
Proč se kolejnice v dálce sbíhají? Důvodem je systém, kterým pracují naše oči. Jelikož naše oči nefungují tunelově, ale máme určitý zorný úhel, je v dálce čím dál více informací, které oko musí zaznamenávat. Proto se s rostoucí vzdáleností objekty "komprimují" a tak máme možnost vidět více. Abychom tohoto efektu mohli dosáhnout i v dvojdimenzionálním světě vznikla lineární perspektiva.
Lineární perspektiva je významnou aplikací středového promítání. V technické praxi se používá především k zobrazování objektů větších rozměrů, napodobuje tak lidské vidění. Ze středu promítání (oka) se objekty promítají do roviny (nahrazuje sítnici). Perspektivní obrazy jsou například fotografie.
Perspektiva v kontextu vidění je definována jako způsob jak se předměty zobrazí relativně k jejich umístění v prostoru a relativně k jejich velikosti. Jinými slovy - je to způsob uspořádání a vzhledu předmětů na snímku tak, aby se napodobilo lidské vnímání prostoru. Základní stavební kameny lineární perspektivy přitom jsou změna velikosti předmětů a sbíhání linií. Sbíhání linií i změna velikosti jsou však rub a líc stejné mince. Prvotní příčina obou jevů je v tom, že čím je předmět dále, tím má menší úhlovou velikost. Přitom právě úhlová velikost předmětu je to, co obraz předmětu reálně tvoří na sítnici oka, na senzoru či filmu.

Abychom dostali názorný obraz odpovídající tomu, co vidí lidské oko, je třeba zavést na středové promítání jisté omezující podmínky.
Středové promítání, které splňuje podmínky 1, 2, 3 se nazývá lineární perspektiva.
Základním principem lineární perspektivy je, že čím jsou předměty dále, tím se pozorovateli jeví menší - zdánlivě tedy mění svojí velikost. Pro příklad uveďme náš Měsíc a naše Slunce. Oba se jeví na obloze zhruba stejně velké - rozuměj mají stejnou úhlovou velikost (úhlový rozměr) kolem 0,5 stupně. Průměr Slunce je však 109 Zemí, kdežto Měsíc má průměr jen 0,3 naší Země. Slunce je tedy asi 400x větší, přesto se na obloze jeví stejně (úhlově) veliké. Příčina je pochopitelně v tom, že Slunce je výrazně dále než Měsíc a tím se jejich úhlové velikosti vyrovnají.
Daný objekt můžeme perspektivně zobrazit buď s využitím jiné zobrazovací metody, pak se lineární perspektiva nazývá vázaná, nebo jen s využitím metod středového promítání, pak se perspektiva nazývá volná.
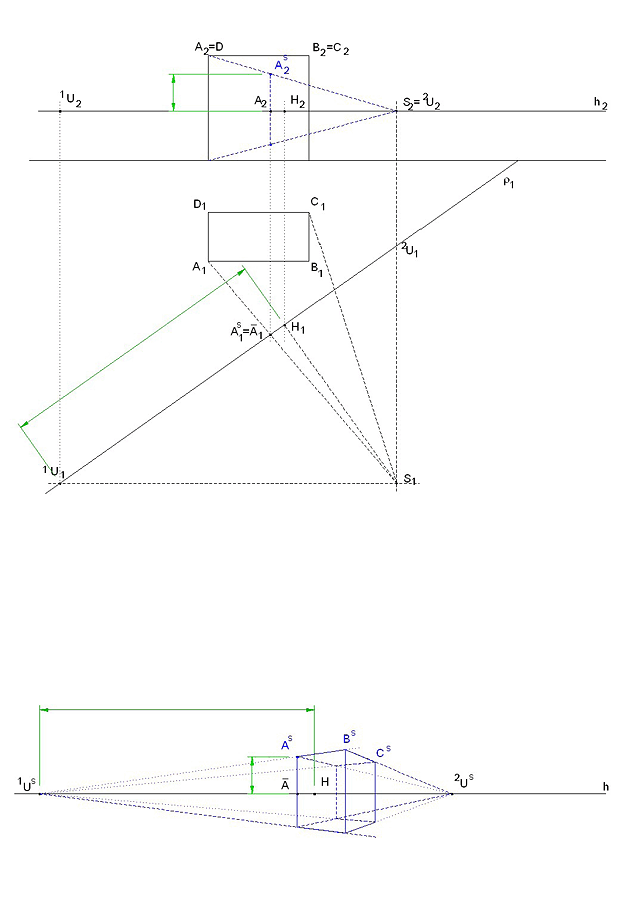
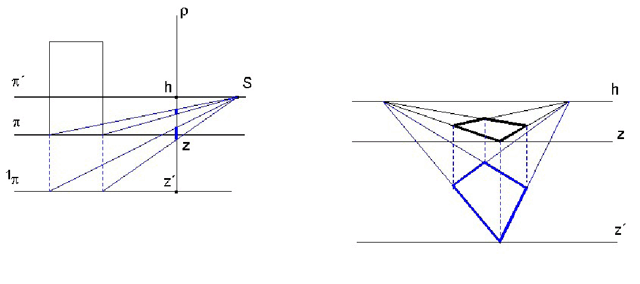
Další nepřímou metodou je stopníková metoda. Opět vycházíme z Mongeovy projekce, ovšem tentokrát volíme objekt vzhledem k soustavě souřadnic tak, aby půdorys byl nad osou x a nárys pod osou x. Objekt stojí na základní rovině (tentokrát ji označíme ξ ) rovnoběžné s π. Průmětnu ρ ztotožníme s nárysnou, perspektiva tedy tentokrát splyne se svým nárysem. Dále zvolíme oko S a horizont h, výška perspektivy by opět měla odpovídat výšce pozorovatele. Aby se nepřekrýval nárys objektu v Mongeově projekci s perspektivou, posuneme nárys ve směru osy x a otočíme do průčelné polohy. Nárys a půdorys si sice neodpovídají v Mongeově projekci, ale pro konstrukce má nárys jen pomocnou roli. Půdorys objektu umístíme tak, aby úběžník aspoň jednoho směru ležel v nákresně. (Například úběžník Ua přímky a=AB.) Sestrojíme hlavní bod a úběžníky některých vodorovných přímek. Sestrojíme perspektivu bodu A. Bod A leží na vodorovné přímce a, její nárys je rovnoběžný s osou x. Určíme nárysný stopník Na přímky a. Na leží v ν (tedy i v ρ) a splývá se středovým průmětem. Perspektiva as přímky a je přímka Uas Na. Na ní leží perspektiva bodu A. Tu sestrojíme takto. Promítneme bod A z S do ρ, půdorys As1 perspektivy As leží na ose x, a protože nárys perspektivy splývá s perspektivou leží As na ordinále a na přímce as. Další body doplňujeme stejně, pokud máme na nákresně úběžníky dalších přímek, můžeme využít i jich.
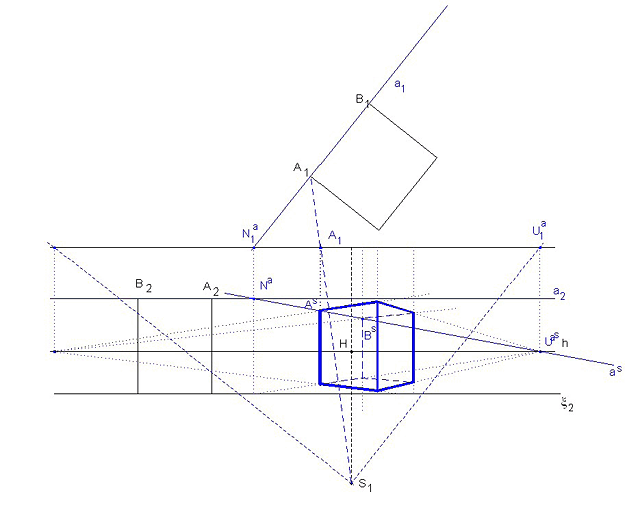
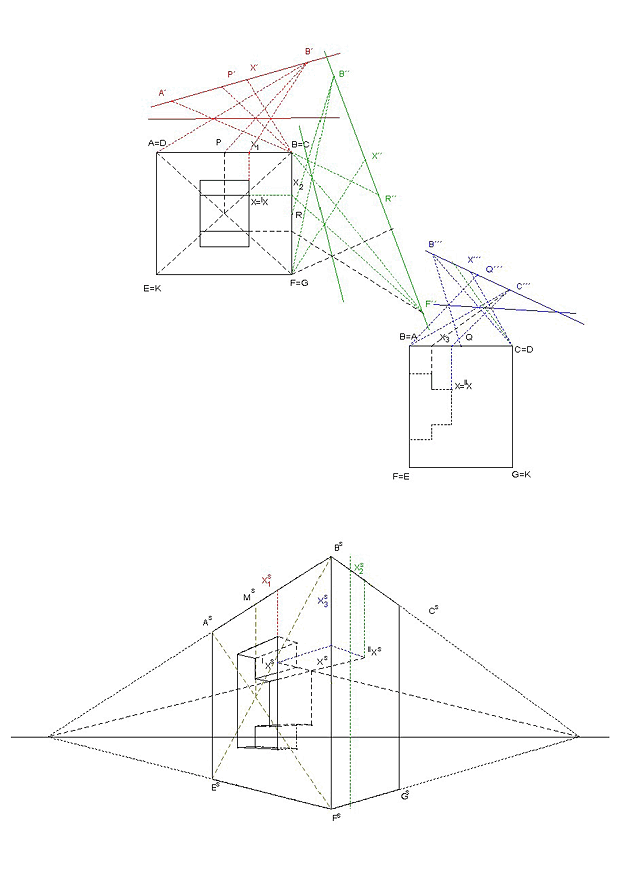
Pro konstrukci složitějších půdorysů můžeme využít další nepřímou metodu a to tzv. incidenční měřítko. Tato metoda využívá Pappovy věty (dvojpoměr se středovým promítáním zachovává). Objekt uzavřeme do kvádru a do jeho stěn pravoúhle objekt promítneme. Kvádr je dán nárysem a bokorysem libovolně v průmětně. Bod X objektu nejprve pravoúhle promítneme do bodu IX ležícího ve stěně ABFE a do bodu IIX ležícího ve stěně BCGF. Bod IX pravoúhle promítneme do bodu X1 na přímce AB a do bodu X2 na přímce BF. Bod IIX pravoúhle promítneme do bodu X3 na přímce BC. Sestrojíme perspektivu kvádru pomocí některé nám zatím známé metody. (V obrázku není znázorněno.) Sestrojíme vhodně přímky A´B´, B´´F´´, B´´´C´´´, které jsou po řadě projektivní a AB, BF,BC, tak, aby platilo IA´B´I=IAsBsI atd. Víme, že projektivita je dána třemi odpovídajícími si páry bodů,sestrojíme proto ještě perspektivy středů P, R, Q úseček AB, BF, BC. (Například pomocí úhlopříček). Můžeme sestrojit bod X´ odpovídající v dané projektivitě bodu X1, bod X´´ odpovídající bodu X2 i bod X´´´ odpovídající bodu X3. (Projektivity v obrázku jsou doplňovány užitím direkční osy, průsečíky přímek AB´ a A´B, BP´ a B´P atd. leží na direkční ose.) Protože platí Pappova věta, platí IAsX1sI=IA´X´I atd. a na perspektivě hran kvádru získáme perspektivy bodů Xi. Body Xi jsme získali pravoúhlým promítáním bodu X do stěn a hran kvádru a jelikož známe úběžníky hran můžeme sestrojit perspektivu bodu X.
Nepřímé metody se používají především v případech, když známe sdružené průměty objektu. Neznáme-li je podrobně a chceme-li perspektivní obraz průběžně doplňovat, opravovat apod., používáme přímé metody.
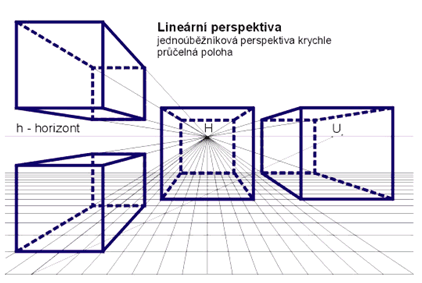
Pokud si zvolíme objekt a chceme sestrojit jeho perspektivu, zvolíme pravoúhlý souřadnicový systém s osami x1, x2, x3 . Souřadnicový systém os je rovnoběžný s hranami zvoleného objektu. Jestli-že objekt při použítí incidenčního meřítka obalíme vhodně zvoleným kvádrem, souřadnicové osy pak budou splývat s hranami kvádru.

Perspektiva je dána horizontem, základnicí a některým z distančníků. Osy budou ležet v základní rovině s označením x1, x2. Souřadnicový systém, který jsme si zvolili nazýváme přidružený k danému objektu. Pokud je průmětna (ρ) zvolena tak, aby byla kolmá k základní rovině, osa x3 je rovnoběžná s průmětnou (ρ). Objekt se zobrazuje v průčelné perspektivě je-li průmětna (ρ) rovnoběžná i s další z os např.: x1. Pouze osa x2 má vlastní úběžník (je hloubková přímka, úběžník je H), a proto se je tato perspektiva pojmenována jako jednoúběžníková. Souřadnicový systém vytvoří čtvercové sítě, poté sestrojíme perspektivu některých těchto sítí.
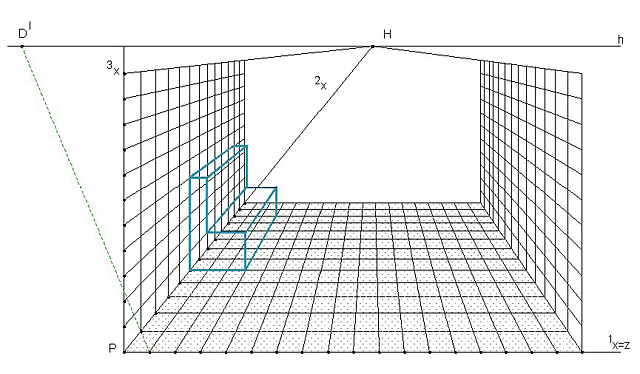
Využití a postup průčelné perspektivy: nejčastěji pro zobrazování interiérů v bytové architektuře, kde sestrojíme perspektivu ve třech vhodných rovinách tj. podlaha a dvě protější stěny kolmé k průmětně (ρ). Osu x1, ztotožníme se základnicí z (leží v ρ, jednotky na ni nanášíme ve skutečné velikosti), osu x3, vedeme libovolným vhodně zvoleným bodem P na z (leží rovněž v ρ, jednotky ve skutečné velikosti). Osa x2, je hloubková přímka, její perspektiva je přímka PH. (Jednotky na ni nanášíme pomocí levého nebo pravého distančníku.) Sestrojíme sítě (jednotkami na osách vedeme rovnoběžky se zbývajícími osami) a s využitím sítí zakreslíme interiér.
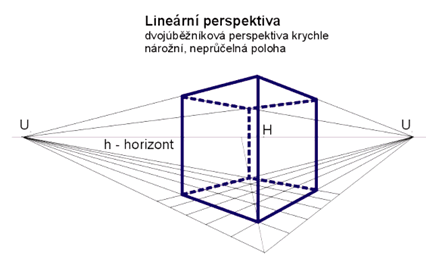
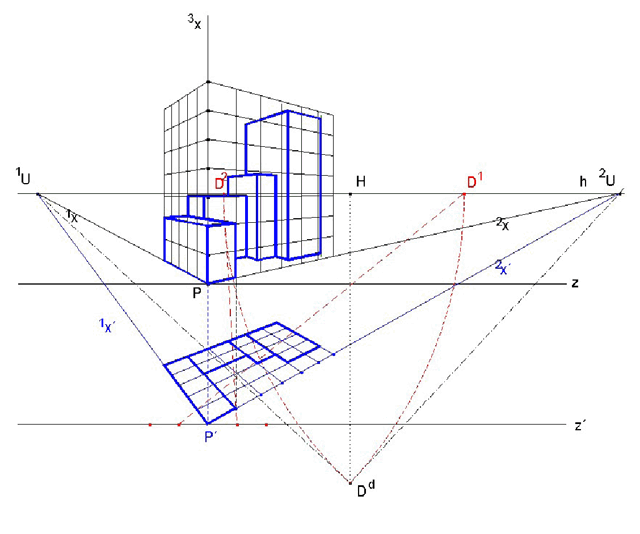
Zobrazovanému objektu opět přiřadíme přidružený souřadnicový systém tak, aby osa 3x byla rovnoběžná s průmětnou ρ. Osy 1x a 2x leží v π, ovšem žádná není rovnoběžná s ρ. Objekt je v nárožní poloze a zobrazujeme jej v tzv. nárožní perspektivě. Protože osy 1x a 2x mají úběžníky 1U, 2U nazýváme někdy tuto perspektivu dvojúběžníková. Zobrazujeme opět čtvercové sítě vhodných rovin a pomocí nich sestrojujeme perspektivu objektu. Nárožní perspektiva se používá především pro zobrazování budov, ulic, komunikací apod. (rozsáhlejší objekty). Protože pozorovatel a objekt stojí na základní rovině, půdorys objektu je vidět pod malým úhlem a tedy velmi zkresleně a při konstrukcích může docházet k větším nepřesnostem. Pro konstrukci čtvercové sítě v půdorysu (a tím i celého půdorysu) používáme tzv. sníženého (sklepního) půdorysu. Zvolíme pomocnou rovinu 1π rovnoběžnou s π ("pod" rovinou π) a půdorys pravoúhle promítneme do 1π´. Je zřejmé, že perspektiva původního půdorysu a sníženého půdorysu si odpovídají v pravoúhlé afinitě s osou h.

Při konstrukci perspektivy objektu sestrojíme perspektivu sníženého půdorysu (čtvercovou síť) a dále čtvercové sítě dané např. rovinami (1x3x) a (2x3x). Zvolíme bod P na z a osu 3x procházející P. (Jednotky na ní budou opět ve skutečné velikosti) Osy 1x a 2x budou procházet bodem P, jejich perspektivy budou přímky P1U, P2U, kde 1U, 2U jsou os 1x, 2x, jeden zvolíme, druhý sestrojíme pomocí sklopení obzorové roviny. Jednotky na osách 1x, 2x sestrojujeme s pomocí jejich dělicích bodů D1, D2. (Známe např. dolní distančník.) Čtvercovou síť sklepního půdorysu můžeme sestrojit buď tak, že sestrojíme na ose 1x jednotky (pomocí dělicího bodu D1, promítáním na z) a ty afinně zobrazíme na 1x´, nebo lze z bodu D1 promítnout přímo na 1x´ jednotky ze z´. Z vlastností afinity je zřejmé, že dostáváme tytéž body.

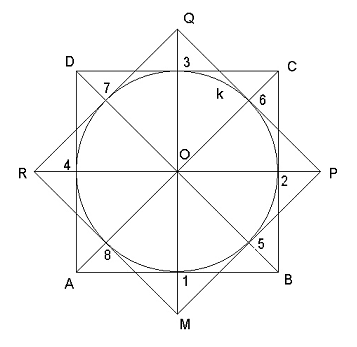
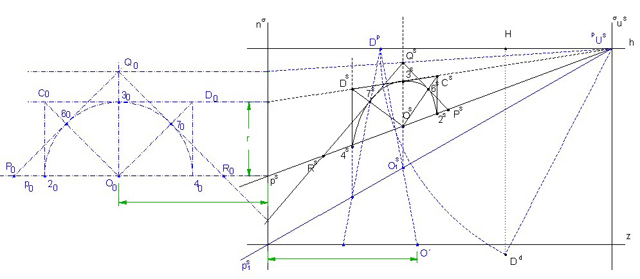
Ve středovém promítání se kružnice, která neleží ve středově promítací rovině, zobrazí jako regulární kuželosečka. Středový průmět kružnice k je řez kužele s vrcholem S a řídící kružnicí k průmětnou. V lineární perspektivě požadujeme, aby zobrazované objekty ležely v zorném poli, tj. uvnitř zorného kužele. Promítací kužel kružnice k leží uvnitř zorného kužele a jeho řez rovinou ρ (průmětna) je elipsa, příp. kružnice. Kružnici v obecné poloze lze zobrazit stejně jako ve středovém promítání, otáčením roviny kružnice do průmětny a užitím kolineace. V lineární perspektivě se nejčastěji zobrazují kružnice ve vodorovné nebo svislé poloze, pro tyto příklady ukážeme konstrukci perspektivy kružnice. Kružnici k opíšeme dva čtverce ABCD a MPQR tak, aby jejich body dotyku (ozn. je 1, 2, …, 8) tvořily pravidelný osmiúhelník. Nejprve zobrazíme kružnici ve vodorovné rovině, např. v základní rovině π. Mějme dán střed O kružnice k a poloměr r. Je perspektiva je opět zadána horizontem, základnicí a některým distančníkem. Opsané čtverce sestrojíme tak, aby strana AB byla rovnoběžná se z. Sestrojíme perspektivy obou čtverců a do nich vepíšeme elipsu (Známe pro ni osm tečen s body dotyku.) Strany nebo úhlopříčky zvolených čtverců jsou buď průčelné nebo hloubkové přímky, úsečky dané délky od body O na ně nanášíme podle známých konstrukcí.
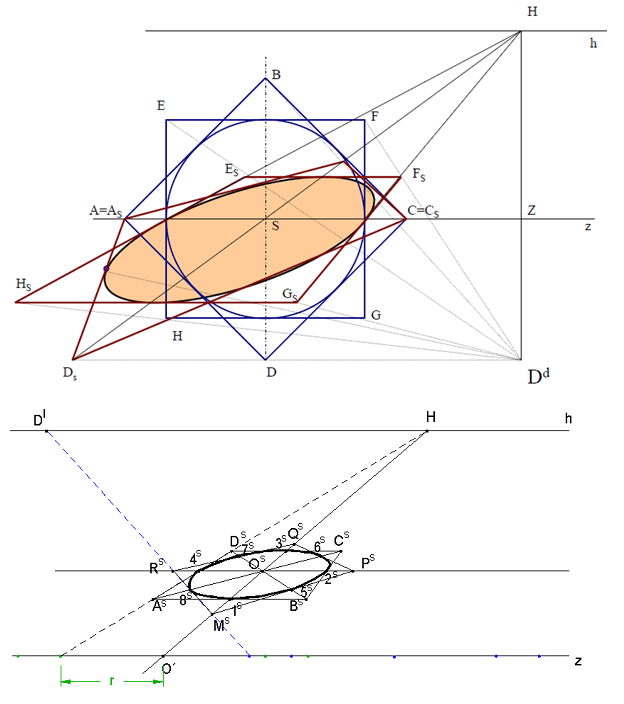
Ve svislé rovině se většinou nezobrazují celé kružnice, pouze jejich části (např. ozdobné štíty domů). Zobrazíme půlkružnici ve svislé rovině σ, která bude dána stopou a úběžnicí. Protože je σ kolmá k π, je stopa i úběžnice kolmá k h. (Perspektiva je zadána stejně jako v předchozím příkladě.) Čtverec dané kružnice opíšeme tentokrát tak, aby strana CD byla rovnoběžná s π. Kružnice je dána středem O (neleží v π) a poloměrem. Přímka p=PR prochází O a je rovnoběžná s π. Promítneme p pravoúhle do roviny π, pravoúhlý průmět označíme p1. Úsečky dané délky nanášíme na přímku ležící v π, tedy na p1 a promítáme opět na p. Známými konstrukcemi sestrojíme perspektivy čtverců a vepíšeme elipsy.
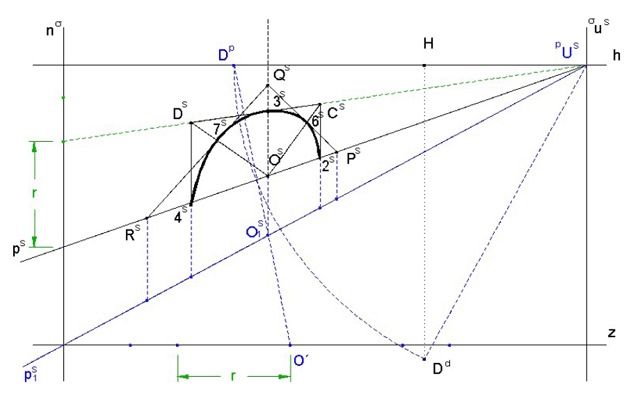
Kružnici lze sestrojit také užitím otočení roviny do ρ1, některé konstrukce se zjednoduší díky tomu, že rovina σ je svislá. Otočené vodorovné přímky jsou rovnoběžné se z, zjistíme vzdálenost bodu O od nárysné stopy (osa kolineace) a sestrojíme na p0 bod O0. Vzdálenost opět zjištujeme na přímce p1. Sestrojíme otočenou půlkružnici a perspektivu některé další svislé přímky, např. procházející bodem D. Na p1 naneseme vzdálenost této svislé přímky od nárysné stopy roviny σ. Perspektivy vodorovných přímek mají společný úběžník, můžeme sestrojit D5C5,7565, odpovídající si přímky se samozřejmě protínají na ose kolineace. Bod D leží na svislé přímce, jejíž vzdálenost od nárysné stopy určíme v otočení, sestrojíme perspektivu svislé přímky. Dále např. bod 3 je průsečík vodorovné přímky CD a svislé přímky jdoucí bodem O. Můžeme sestrojit např. bod Q, jako průsečík vodorovné a svislé přímky, známe průsečík přímky Q0R0 s osou kolineace, sestrojíme perspektivu přímky QR atd.