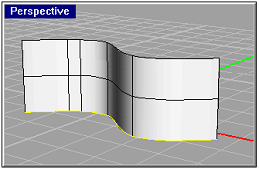
Obr. 1.1 - Translační plocha vzniká vytažením tvořící křivky přímo
Plochu lze vytvořit spojitým pohybem křivky, která není trajektorií tohoto pohybu. Tvar křivky se může během pohybu i měnit.
Polochy k1,k2,... pohybující se křivky odpovídají hodnotám u1,u2,... parametru u . Plocha je jednoparametrická soustava křivek v prostoru.
Každá z tvořících křivek k1,k2,... plochy je jednoparametrickou soustavou bodů závislých na dalším parametru v . Plocha je tedy dvouparametrická soustava bodů v prostoru.
Plocha vzniká pohybem křivky, proto nás zajímají dva způsoby klasifikace ploch:
| název plochy | pohyb | příklad plochy |
| translační | posunutí | válec, rovina |
| rotační | rotace | rotační válec, rotační kužel, rotační hyperboloid |
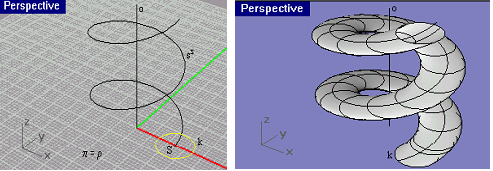
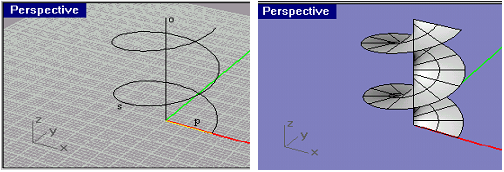
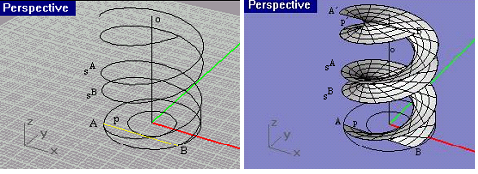
| šroubové | šroubový pohyb | cyklická šroubová plocha, vývrtková šroubová plocha |
| názav plochy | křivka | příklad plochy |
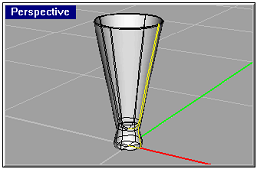
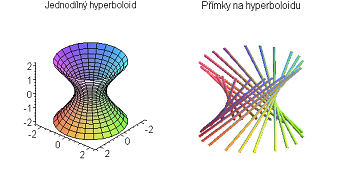
| přímkové | přímka | kuželová plocha, hyperbolický paraboloid, přímkové šroubové plochy |
| cyklické | kružnice | válec, Archimédova serpentina |
| jiné | jiná křivka | kvadriky, obalové plochy |
Plocha v E3 je množina X [x,y,z] bodů, jejichž souřadnice jsou vyjádřeny soustavou rovnic
x = x (u, v)
y = y (u, v)
z = z (u, v)
přičemž u a v jsou parametry. Každou dvojici u a v z určitého Ω oboru nazýváme bodem plochy za předpokladu, že tyto rovnice mají dostatečný počet spojitých nebo po částech spojitých derivací prvního řádu podle u a v.
Pokud lze tyto rovnice převést na tvar
z = f (x, y)
pak se jedná o explicitní rovnice plochy.
Implicitní rovnice má pak tvar F(x, y, z) = 0
Určují vztah mezi derivacemi vektorů n (normála) a r (rádiusvektor)
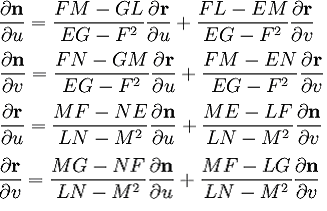
E, F, G jsou základní veličiny plochy prvního řádu
L, M, N jsou základní veličiny plochy druhého řádu
Umožňuje určit druhou derivaci vektoru r
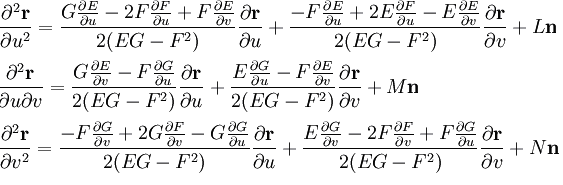
E, F, G jsou základní veličiny plochy prvního řádu
L, M, N jsou základní veličiny plochy druhého řádu
Určují vztah mezi základními veličinami plochy prvního řádu a druhého řádu
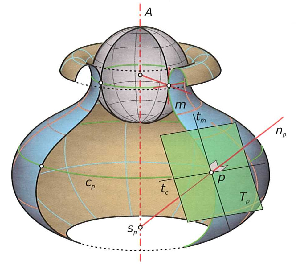
tečná rovina Tp rotační plochy v bodě p je dána tečnou tc rovnoběžkové kružnice a tečnou tm meridiánu
normála np rotační plochy v bodě p protíná osu
v regulárním bodě plochy všechny její tečny leží v jedné rovině, tzv. tečné rovině plochy
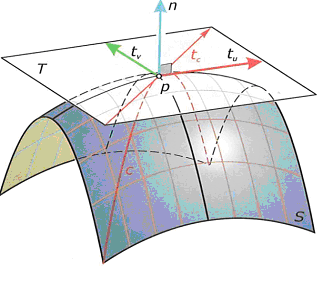
tečná rovina v bodě (u0,v0) je generována (např.) tečnami parametrických křivek se směrovými vektory
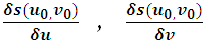
normála plochy je kolmice na tečnou rovinu v bodě dotyku
směrový vektor normály n v bodě P=(u0,v0)=[x0,y0,z0] je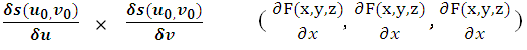 
x=x0, y=y0 , y=y0
pokud v parametrickém vyjádření plochy S nahradíme parametry u, v funkcemi
u=u(t), t ∈ I
v=v(t)
dostaneme rovnice křivky na ploše S
c(t)=(x(t), y(t), z(t))
tečna tc křivky c na ploše S je tečnou plochy S
bod, v němž nelze jednoznačně sestrojit tečnou rovinu, se nazývá singulární bod
ostatní body se nazývají regulární
např. pro plochu c(u, v) = (u,u2,uv) dostáváme dvě tečné roviny podél osy y obdobně vrchol kuželové plochy je singulární bod
i v blízkosti tečného bodu muže tečná roviny obsahovat více společných bodu s plochou než jen bod dotyku
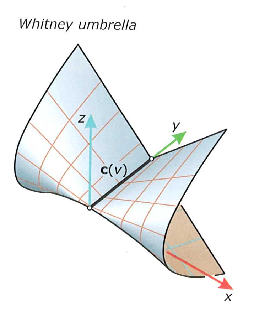
podle chování „v okolí“ rozlišujeme body na eliptické, hyperbolické a parabolické
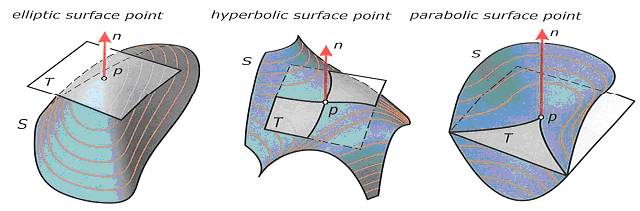
plochu protneme rovinou obsahujícím danou normálu n v bodě P > získáme průsečnou křivku s křivostí kn (normálová křivost ve směru u)
existují dva na sebe kolmé směry, v nichž je normálová křivost maximální a minimální, tzv. hlavní směry a hlavní křivosti k1, k2
x = x (u(t), v(t))
y = y (u(t), v(t))
z = z (u(t), v(t))
u (t), v (t) jsou funkce na intervalu I s dostatečným počtem derivací na I.
u – křivky:
x = x (u, v0)
y = y (u, v0)
z = z (u, v0)
kde v0 je konstanta a u ∈ I
v – křivky:
x = x (u0, v)
y = y (u0, v)
z = z (u0, v)
kde u0 je konstanta a v ∈ I
Tyto křivky tvoří poté na ploše souřadnicovou síť.
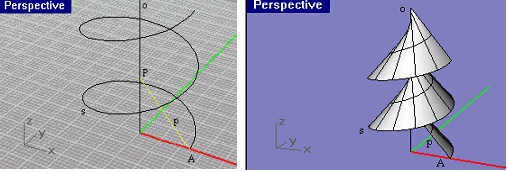
Rotační plochu vytvoří křivka k otáčením kolem přímky o. Předpokládáme, že tvořící křivka k není součástí osy o otáčení ani neleží v rovině kolmé k ose o. Osu o otáčení nazýváme osa rotační plochy.
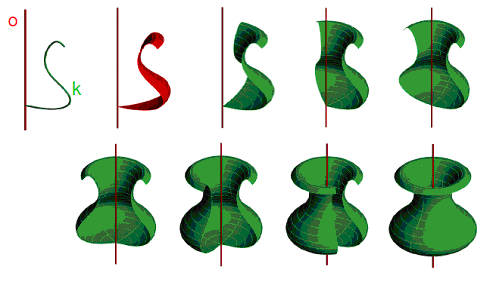
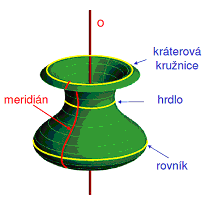
Rotační plochu lze vytvořit pomocí různých tvořících křivek. Jednotlivé body tvořící křivky k opisují kružnice na ploše, tzv. rovnoběžky. Každá rovina procházející rotační osou protíná rotační plochu v křivce, která se nazývá meridián (všechny meridiány rotační plochy jsou vzájemně shodné křivky).
Rovník - jestliže tečny podél této rovnoběžky tvoří rotační válcovou plochu a poloměr je lokálním maximem, tj. ze všech okolních rovnoběžek je tento poloměr největší
Hrdlo - jestliže tečny podél této rovnoběžky tvoří rotační válcovou plochu a poloměr je lokálním minimem, tj. ze všech okolních rovnoběžek je tento poloměr nejmenší
Kráterová kružnice - jestliže tečny podél této rovnoběžky tvoří rovinu, tj. bod ve kterém je tečna tvořící křivky kolmá k ose plochy.
Tvořící křivku c(u)=[x(u),y(u),z(u)] podrobíme rotačnímu pohybu kolem osy z:
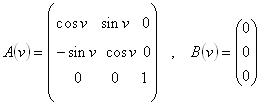
Analytický popis odpovídající rotační plochy je
x(u,v)=x(u)cos v - y(u)sin v
y(u,v)=x(u)sin v + y(u)cos v
z(u,v)=z(u)
Pokud je tvořící křivkou meridián ležící v rovině xz, m(u)=[x(u),0,z(u)] , je parametrické vyjádření:
x(u,v)=x(u)cos v
y(u,v)=x(u)sin v
z(u,v)=z(u)
X(u,v)=[x(u).cos v, x(u).sin v, z(u)]
Plochu můžeme zapsat implicitně ve tvaru F(x,y,z) = 0.
(např. x2/4 + y2/4 + z2 - 1 = 0 ⇒ rotační elipsoid)
x2/a2+y2/a2+z2/b2=1 ⇒ zploštělý rotační elipsoid (a2>c2)
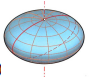
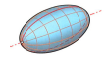
x2/a2+y2/a2+z2/b2=1 ⇒ protáhlý rotační elipsoid (a2 <, c 2)
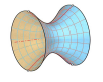
x2/a2+y2/a2-z2/b2=1 ⇒ jednodílný rotační hyperboloid
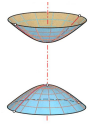
x2/a2+y2/a2-z2/b2=-1 ⇒ dvojdílný rotační hyperboloid
x2/a2+y2/a2=z ⇒ rotační paraboloid
Průnikovou křivku dvou rotačních ploch konstruujeme zpravidla bodově. Obě rotační plochy protneme vhodnou pomocnou plochou, jejíž průniky s danými plochami lze snadno zkonstruovat. Společné body těchto průnikových křivek jsou již body hledaného průniku. Volba soustavy pomocných ploch závisí také na vzájemné poloze os obou rotačních ploch.
Nechť rotační plochy mají společnou osu. Mají-li takové dvě plochy společný bod A, který neleží na společné ose rotace, mají společnou také rovnoběžku, kterou při rotaci opíše bod A. Je-li společná osa rovnoběžná s průmětnou, průniková kružnice se zobrazí do úsečky kolmé k průmětu osy. Například průnik rotační kuželové plochy a kulové plochy, jejíž střed leží na ose kuželové plochy (a která neprochází vrcholem kuželové plochy), jsou dvě kružnice.
Rovina σ , určená oběma osami, je společnou rovinou souměrnosti obou ploch, a tedy i rovinou souměrnosti průnikové křivky. Za pomocné plochy volíme roviny kolmé k oběma osám. Pomocné roviny protínají dané plochy v rovnoběžkách; jejich společné body průniku.
Pravoúhlým průmětem průnikové křivky do roviny kolmé k osám je osově souměrná křivka. Je-li průmětna rovnoběžná se společnou rovinou souměrnosti obou ploch, kolmým průmětem průnikové křivky do této průmětny je dvojnásob počítaná křivka (každý její bod je průmětem dvou bodů průnikové křivky).
Za pomocné plochy volíme kulové plochy se středem v průsečíku daných rotačních ploch. Pomocné kulové plochy volíme tak, aby každou z daných ploch proťaly aspoň v jedné rovnoběžce. Průniková křivka je souměrná podle roviny σ obou os. Pravoúhlým průmětem průniku na rovinu rovnoběžnou s rovinou σ je dvojnásobně počítaná křivka.
Snažíme se volit pomocné roviny tak, aby protínaly dané plochy pokud možno v jednoduchých křivkách (nejvhodněji v přímkách nebo kružnicích). Tak např. rovina kolmá k ose jedné plochy protíná tuto plochu v kružnici. Je-li její řez s druhou plochou jednoduchou křivkou, stačí za pomocné roviny volit roviny rovnoběžné se zvolenou rovinou. Není-li řez s druhou plochou jednoduchou křivkou, volíme rovinu kolmou k druhé ose a vyhledáme řez s první plochou. Jestliže ani tento řez není jednoduchá křivka, pak zpravidla za pomocné roviny volíme roviny rovnoběžné s oběma osami.
Ve speciálním případě, kdy jedna rotační plocha je anuloid a druhá má osu v rovině kružnice s, kterou vyplní středy meridiánů anuloidu, lze průnik snadno sestrojit užitím vhodně volených pomocných kulových ploch. Kulová plocha, která prochází polomeridiánem m anuloidu a má střed na ose rotační plochy, protíná totiž rotační plochu v kružnicích, jejichž společné body s polomeridiánem m jsou body průniku.
Průnikem kvadratických ploch je prostorová kvadrika; jejím průmětem je rovinná kvadrika. Mají-li dané kvadriky společnou rovinu souměrnosti, pak každé dva body průnikové křivky, které jsou souměrně sdružené podle této roviny, promítají se v pravoúhlém promítání na rovinu rovnoběžnou se společnou rovinou souměrnosti do jednoho bodu. Odtud plyne: Pravoúhlý průmět průnikové křivky dvou kvadrik na rovinu rovnoběžnou se společnou rovinou souměrnosti obou kvadrik je kuželosečka (popř. její oblouky).
Rotační kvadriky s různoběžnými osami 1o, 2o mají rovinu 1o2o za společnou rovinu souměrnosti, a tedy podle předchozí věty speciálně platí: Pravoúhlý průmět průnikové křivky dvou rotačních kvadrik s různoběžnými osami na rovinu rovnoběžnou s rovinou os je kuželosečka (popř. její oblouky).