Topografické plochy jsou speciální grafické křivky, které slouží v technické praxi jako nahrazení zemského povrchu, který je obvykle velmi členitý a tudíž ho nelze přesně matematicky vyjádřit.
jsou zadávány soustavou výškově kótovaných bodů nebo vrstevnicemi, zobrazením zemského povrchu do roviny se zabývá kartografie
k zobrazení topografických ploch používáme především kótované promítání, kde průmětnou je mořská hladina, na kterou promítáme kolmo
aby nedocházelo ke zkreslení v průmětu plochy, můžeme takto zakreslit pouze malou část zemského povrchu (do 200 km2), kde můžeme zanedbat zakřivení zeměkoule.
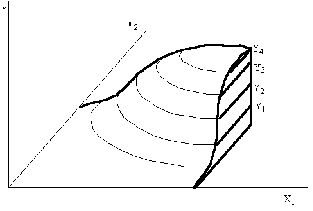
Topografická plocha je dána soustavou křivek – vrstevnic.
je čára, která spojuje body o stejné nadmořské výšce a leží ve vodorovné rovině s průmětnou (horizontála)
jedná se o řezy terénu vodorovnými rovinami s vyznačením jejich výšek (kót)
souhrn všech vrstevnic nazýváme vrstevnicovým plánem

Obr. 1 – soustava rovnoběžných rovin
Vzdálenosti rovnoběžných rovin, kterými promítáme zemský povrch, jsou udávány v metrech. Pro danou plochu jsou tyto roviny vždy ekvidistantní (mají stejnou vzdálenost), přičemž jejich vzdálenost (ekvidistance) je závislá na členitosti terénu, velikostí části zobrazované plochy a použitým měřítkem.
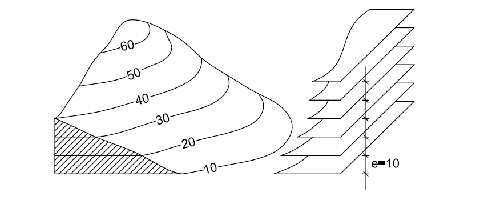
Obr. 2 – zobrazení ekvidistantních rovin
Udává v jakém poměru bude zobrazena úsečka d změřená na mapě k odpovídající délce D ve skutečnosti
M = d/D
Topografické plochy můžeme rozdělit podle zobrazení:
mapy – je zmenšené znázornění objektů na Zemi, skutečné vzdálenosti na mapě se obvykle zobrazují ve velkém měřítku (např.: 1:500 000)
Obr. 3 – příklad topografické mapy
plány – slouží především k zobrazení projektovaných objektů nebo území (územní plán), například dopravní stavby (silnice, železnice) se zobrazují v malém měřítku v malém měřítku (např.: 1:1000)
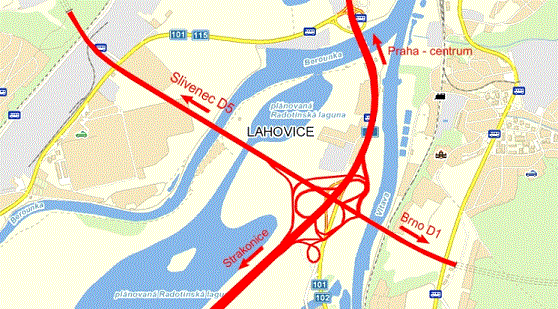
Obr. 4 – plán řešení mimoúrovňové křižovatky pražského obchvatu v Lahovicích
Topografické plochy jsou dány soustavou vrstevnic, tvořící vrstevnicovým plánem a měřítkem, ve kterém jsou zobrazované.
Křivky, vyskytující se na topografické ploše, můžou být:
spádová (spádnice) – křivka spojující dva body, které leží ve směru jejího největšího spádu (protíná všechny vrstevnice v pravém úhlu)
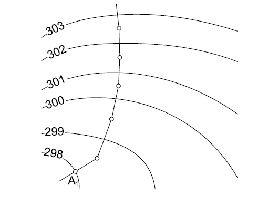
Obr. 5 – spádová přímka (spádnice)
křivka stálého pádu – nazýváme čáru, která má v každém svém bodě stejný spád. Tuto křivku můžeme nahradit lomenou čárou, skládající se ze stejně velkých úseků i => úseky lomené čáry jsou mezi vrstevnicemi stejné a rovnají se intervalu i
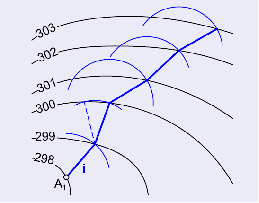
Obr. 6 – křivka konstantního spádu
hřebenová (úboční) – zvláštní případ spádové křivky, z každého bodu hřebenové křivky vycházejí zpravidla dvě spádnice, které směřují od hřebenové křivky
udolní (údolnice) – jedná se o opačný případ než u hřebenové křivky, kdy sousední spádnice směřují k údolní křivce z obou stran
hřbetní (hřbetnice) – vzniká, když je TP zobrazena vrstevnicemi, které mají ostré lomy, spojnice bodů sousedních vrstevnic tvoří hřbetnici, která je hranou TP
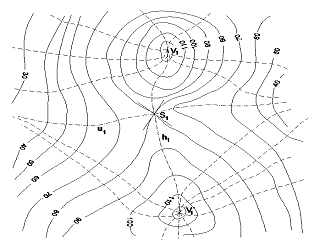
Obr. 7 – h1 – hřbetní křivka (hřbetnice); u1 – údolnice; V1 – vrcholy; S1 – vrchol sedla
vrstevnice – křivka spojující 2 body, jejichž kóty jsou stejná čísla
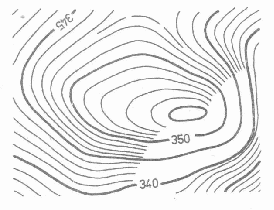
Obr. 8 – vrstevnicový plán
Obr. 9 – aplikace bodů a křivek v topografické mapě
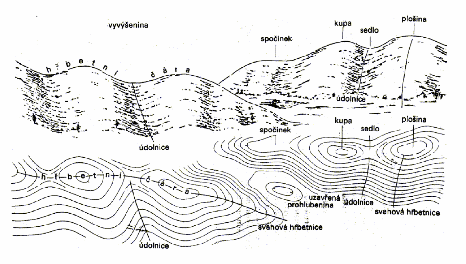
vrchol – tečná rovina v bodě V (vrchol) je vůči topografické ploše vodorovná s tím, že v okolí bodu V je celá topografická plocha pod tečnou rovinou vrcholu
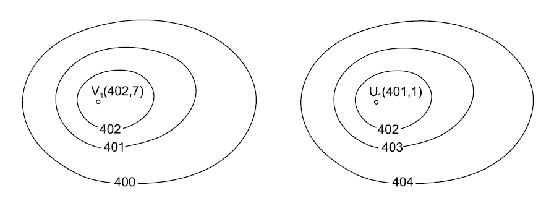
Obr. 10 – vrchol a údolí
údolní bod – tečná rovina v bodě U (údolí) je vůči topografické ploše taktéž jako vrchol vodorovná, ovšem oproti vrcholu se tečná rovina v okolí bodu U nachází pod celou topografickou plochou
sedlo- bod S se nazývá vrchol sedla, tečná rovina v bodě S je vůči topografické ploše vodorovná. Tečná rovina sedla v bodě S protíná topografickou plochu ve dvou vrstevnicích
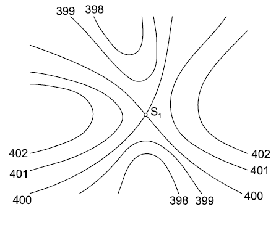
Obr. 11 – sedlo v topografické mapě (bod S)
Rovinu označujeme nákresnu (plocha, na kterou se kreslí), nebo rovinný útvar (polorovina, rovinný úhel, křivka). Značí se malým řeckým písmenem.
Rovinný řez topografickou plochou je obecná křivka. Její jednotlivé body jsou průsečíky hlavních přímek, což jsou vlastně vrstevnice dané roviny, a vrstevnic topografické plochy o stejných kótách.
Př: Sestrojte řez roviny topografickou plochou. Rovina je daná spádovým měřítkem.
Řešení:
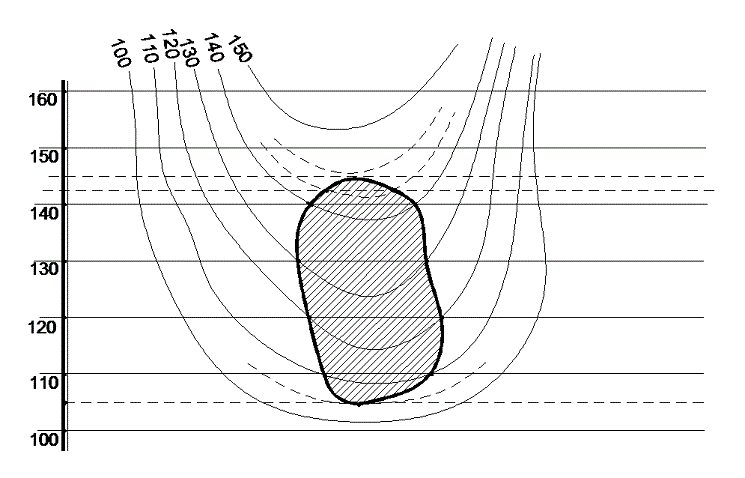
Obr. 12 – řez roviny
1) sestrojíme průměty vrstevnic roviny kolmo ke spádovému měřítku (hlavní přímky roviny); 2) určíme jejich průsečíky s vrstevnicemi o stejných kótách; 3) dostaneme jednotlivé body průnikové křivky, které spojíme plynulou čarou (obr. 12); 4) Části řezu mezi vrstevnicemi 150, 140 a 110, 100 určíme pomocí interkalárních vrstevnic (čárkované vrstevnice), které sestrojíme na ploše i v rovině; 5) výsledkem je vyšrafovaná plocha na obr. 12.
Řez svislou rovinou spočívá v protnutí topografické plochy rovinou kolmou k půdorysně, tedy kolmou i k ostatním vrstevním rovinám. Tím získáme průsečnou křivku k, kterou nazýváme profilem. Půdorys křivky splývá s půdorysnou stopou roviny řezu. Skutečný tvar profilu tedy získáme sklopením roviny řezu do průmětny kolem její stopy, nebo sklopením kolem hlavní přímky této roviny do vrstevní roviny, která touto hlavní přímkou prochází.
Pomocí příčného profilu získáme lepší představu o tvaru topografické plochy v daném směru.
Př. Sestrojte příčný profil topografické plochy ve směru PQ. Bod P leží na vrstevnici o kótě 40 a bod Q na vrstevnici o kótě 50.
Řešení:
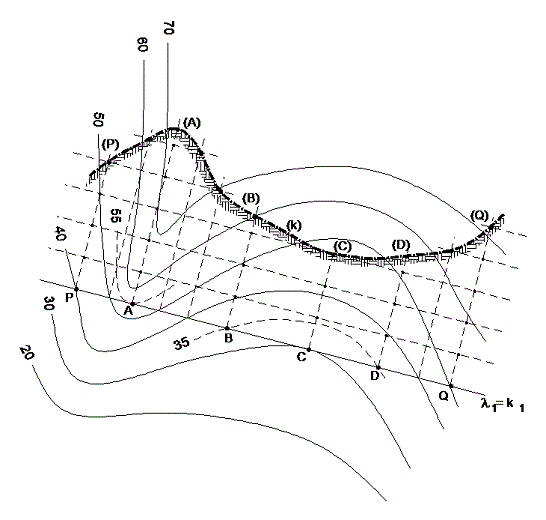
Obr. 13 – příčný profil
1) spojením bodů P a Q získáme půdorysnou stopu svislé roviny λ splývající s půdorysem křivky řezu k; 2) rovinu λ sklopíme do průmětny kolem půdorysné stopy tak, že sklopíme postupně průsečíky křivky k s jednotlivými vrstevnicemi; 3) získané body spojíme křivkou s (obr. 13), k přesnějšímu sestrojení křivky s určíme mezi vrstevnicemi 30 a 40 a vrstevnicemi 50 a 60 interkalární vrstevnice, jež protnou půdorys roviny řezu v bodech A, B a D.
Máme-li prostorovou křivku, kterou rozvineme do roviny, můžeme získat podélný profil. Určíme ho tak, že každým bodem křivky k vedeme promítací paprsek. Promítací paprsky vytvoří promítací válcovou plochu dané křivky, která protne topografickou plochu právě v křivce k. Válcovou plochu sklopíme do průmětny. Nejdříve rozvineme křivku k do přímky tak, že ji rozdělíme na dostatečný počet stejně velkých oblouků. Ty pak nahradíme jejich tětivami, jejichž velikost vyneseme na přímku. Na kolmice vedené k přímce vyneseme pomocí kót jednotlivé body. Plynulým spojením bodů vznikne podélný profil. Podle potřeby, stejně jako u příčného profilu, můžeme sestrojit zvýšený nebo snížený podélný profil. Podélný profil se využívá k vyšetřování průběhu cesty, železnice, či vodního toku, hlavně pokud se týče výškových poměrů ve směru dané křivky.
Př: Sestrojte podélný profil topografické plochy mezi body A, B ve směru dané křivky k.
Řešení:
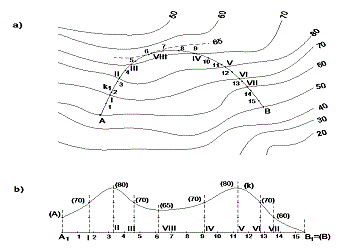
Obr. 14 a) – vedení trasy v topografické ploše
Obr. 14 b) – podélný profil dané trasy
1) nahradíme půdorys křivky k lomenou čarou; 2) Nanášíme stejné úsečky |A1|
= |12| = … = |14 15| na libovolně zvolenou přímku mimo vrstevnicový plán; 3) Body I, II, … ,VII, kde křivka k protne vrstevnice terénu, vyznačíme v rozvinutí přenesením příslušného oblouku křivky z půdorysu na přímku; 4) křivku k1 v rozvinutí sklopíme, pomocí rozdílů kót, do pomocné průmětny o kótě 50
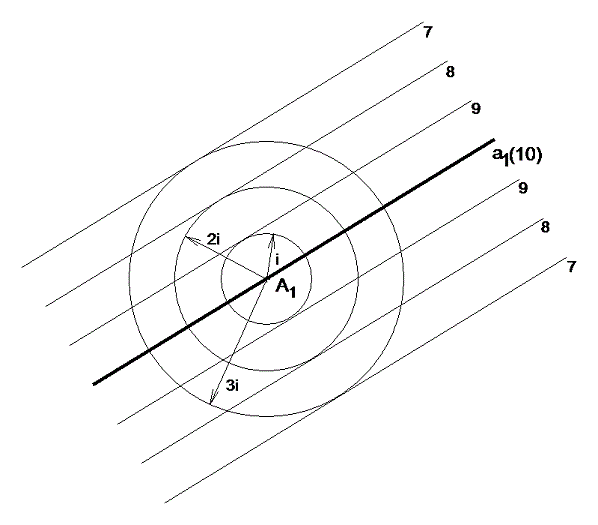
Křivka konstantního spádu
Př : Daným bodem M na topografické ploše sestrojte křivku k stálého spádu tg α
Řešení:
Pro jednoduchost bude ležet bod M na vrstevnici 40 topografické plochy.
1) sestrojíme na pomocném náčrtku interval i daného spádu nebo je možné ho spočítat, jelikož i = cotg ;; 2) kolem bodu M(40) opíšeme kružnici o poloměru i; 3) kružnice protne vedlejší vrstevnice 30 a 50 v bodech 1, 2, 3, 4; 4) kolem každého z těchto bodů také opíšeme kružnici s poloměrem i, která vytne body 5, 6 na vrstevnici 60, tuto konstrukci dále opakujeme. Body, které získáme, pak spojujeme lomenou čarou (ovšem kružnice o poloměru i kolem bodu 4 se nám s vrstevnicí 60 neprotne, což znamená, že v bodě 4 křivka nepokračuje).
Je vidět, že z daného bodu lze vést několik cest, které mají určený spád. Z těchto možných výsledků, pak zvolíme tu nejvýhodnější a podle potřeby ji zaoblíme.
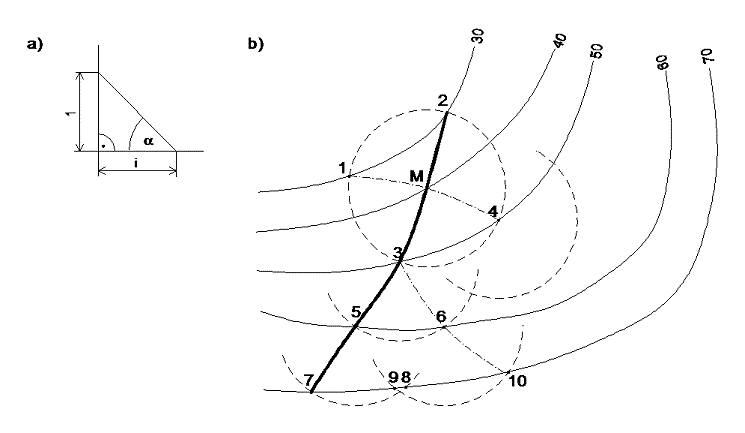
obr. 15 – křivka konstantního spádu
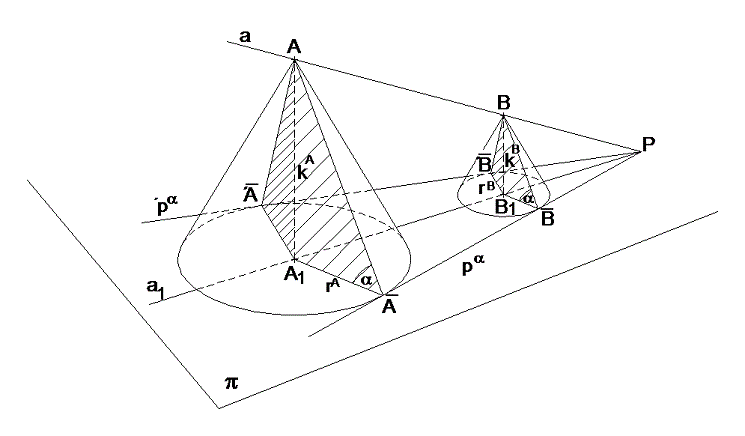
Plochou konstantního spádu rozumíme přímkovou plochu, jejíž tečné roviny svírají s horizontální rovinou předepsaný úhel.
Všechny přímky, které procházejí daným bodem A a s promítací rovinou svírají daný úhel, tvoří plochu rotačního kužele s vrcholem v bodě A a osou kolmou na danou promítací rovinu.
Vrstevnicový plán tohoto spádového kužele dostaneme zobrazením jeho řezů s vrstevnicovými rovinami. Jsou jím tedy soustředné kružnice se středem A1. Jejich poloměry se liší o iα, tedy o délku intervalu průmětu přímky s daným spádem (obr. 4.1.1).
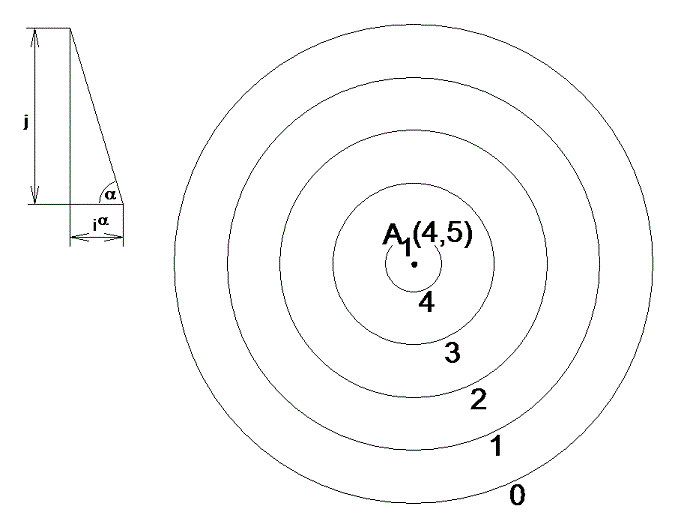
obr. 16 – spádový kužel
Každým bodem dané přímky můžeme sestrojit spádový kužel. Společná obalová plocha těchto kuželů je hledaná plocha konstantního spádu přímky.
Daná plocha se tedy musí dotýkat každého spádového kužele podél jeho určité povrchové přímky. Musí však také obsahovat danou přímku, jako množinu vrcholů všech spádových kuželů. Plochami konstantního spádu přímkou jsou tedy dvě roviny, které mají předepsaný spád (obr. 16).
Obr. 16 – zobrazení plochy konstantního spádu přímkou
Je-li daná přímka rovnoběžná s průmětnou α, procházejí jí opět dvě roviny předepsaného spádu, které jsou vzhledem k α antiparalelní, zadaná přímka je jejich hlavní přímkou (obr. 17).
obr. 17 – přímky rovnoběžné s průmětnou
Je-li přímka kolmá k průmětně, nemá tato úloha smysl.
Pokud daná přímka a není ani rovnoběžná, ani kolmá k ß a máme -li zadán vystupňovaný průmět přímky a spád tg ß hledané plochy, řešíme úlohu takto.
Řešení:
obr. 18 – přímka se zadaným spádem
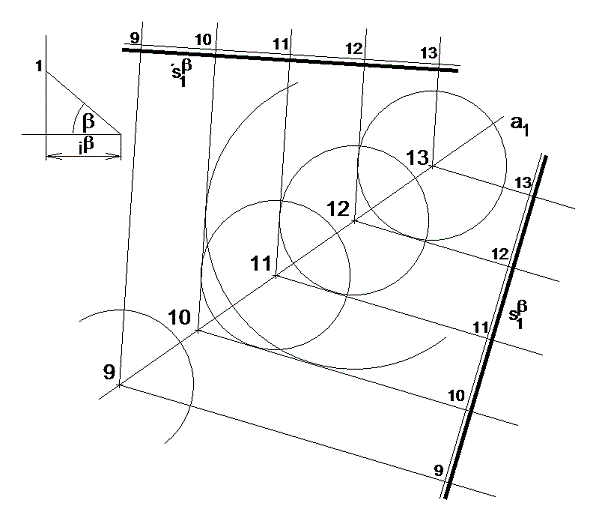
1) určíme jednu vrstevnicovou rovinu (např. kóty 10) za rovinu ß´ a zjistíme průsečík této roviny s přímkou a a kružnice, ve kterých spádové kužely bodů přímky a protínají ß´.
2) v tomto případě jsou to kružnice s poloměrem iß a středem v bodě kóty 11, kružnice s poloměrem 2ißa středem v bodě 12, atd. (obr. 18); 3) tečny sestrojené z průsečíku přímky a s ß´ ke kružnicím jsou hlavními přímkami hledaných rovin daného spádu tg ß (obr. 4.1.4).
Pokud tuto úlohu řešíme pro případ násypové plochy, určíme tečny z bodu o určité kótě k ke kružnici, která má střed v bodě o kótě k+1 (obr. 19 a) ). V případě výkopové plochy sestrojujeme tečny z bodu kóty k ke kružnici se středem o kótě k-1 (Obr. 19 b) ).
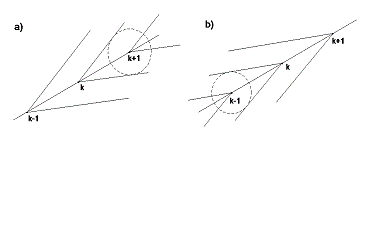
Obr. 19
Tato plocha je složena z částí rovin daného spádu přímky, na které leží daná úsečka, a z částí spádových kuželů koncových bodů úsečky. Společné tečny kružnic o stejných kótách v průmětu jsou hlavními přímkami rovin hledaného spádu (obr. 20).
Na obr. 20 a) je tato úloha řešena pro násyp a na obr. 20 b) pro výkop. Délka intervalu násypové plochy je in a délkou intervalu výkopové plochy je iv (obr. 20).
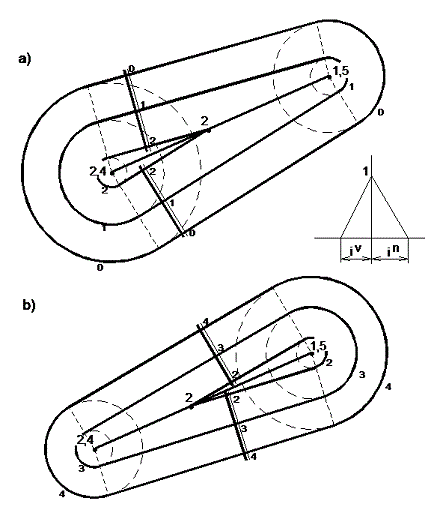
Obr. 20
Úloha na sestrojení plochy konstantního spádu lomenou čarou je vlastně několikerým opakováním předešlé úlohy.
Plochu daného spádu jsme také sestrojili z částí rovin a z částí spádových kuželů koncových bodů lomené čáry (obr. 21).
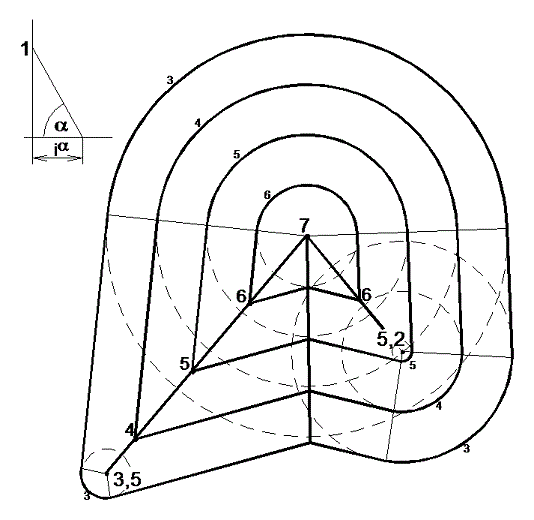
obr. 21 – plocha konstantního spádu lomenou čarou
Hledaná plocha se musí dotýkat spádových kuželů každého bodu dané křivky, podél celé povrchové přímky. Tato přímka je společná kuželové ploše a rovněž ploše konstantního spádu. Podél této přímky mají tedy společnou tečnou rovinu, která prochází i vrcholem kužele. Proto také prostorová křivka, která je množinou všech vrcholů, leží na hledané ploše. Rovněž tečna křivky je obsažena ve společné tečné rovině spádového kužele a plochy konstantního spádu. Touto tečnou je možno vést k dané kuželové ploše dvě tečné roviny, které se dotýkají kužele v povrchových přímkách, jež jsou také přímkami hledané plochy konstantního spádu.
Př. 4.1.1 : Sestrojte plochu konstantního spádu tg α k prostorové křivce k, která je dána svým vystupňovaným průmětem.
Řešení:
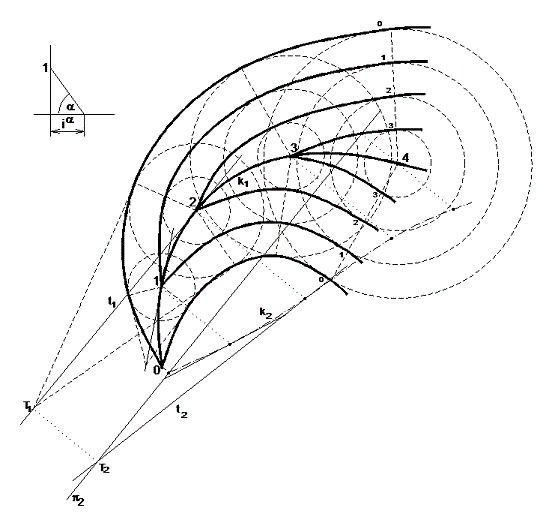
obr. 22 – plocha konstantního spádu prostorovou křivkou
1) sestrojíme jednotlivé spádové kužely bodů o celočíselných kótách na křivce k; 2) v bodě o kótě 2 sestrojíme tečnu t k této křivce (obr. 22); 3) dále je nutné sestrojit stopník této tečny v rovině o kótě 0, či jiné vhodné vrstevnicové rovině mimo rovinu kóty 2; 4) K tomu použijeme druhý průmět křivky k do roviny kolmé k α; 5) v tomto druhém průmětu sestrojíme sdružený průmět t2 tečny t a na něm najdeme druhý průmět T2 bodu T, v němž protíná tečna průmětnu α (obr. 22). První průmět T1 leží na t1 a zároveň na kolmici z T2 k druhému průmětu α2. Stopy tečných rovin jsou tečnami z bodu T1 ke kružnicím o kótě 0 spádového kužele v bodě 2. Spojíme-li dotykové body na této kružnici s bodem 2, získáme povrchové přímky hledané plochy (obr. 22). Tento postup opakujeme ve všech bodech o celých kótách křivky k. Vrstevnice výsledné plochy jsou křivky, které spojují body o stejných kótách na povrchových přímkách.